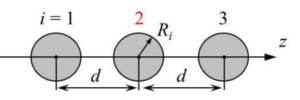
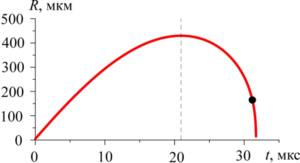
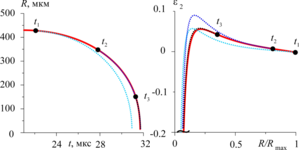
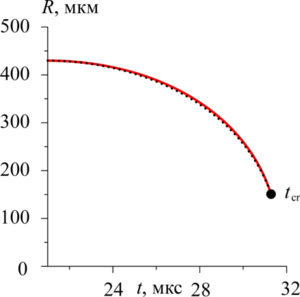
A mathematical model and a numerical technique for studying strong expansion and collapse of cavitation bubbles located in the central region of a streamer where the bubbles are almost motionless are developed. They are essentially efficient combinations of the models and techniques previously created by the authors for calculating the dynamics of interacting weakly-non-spherical bubbles in a streamer and the dynamics of a single axisymmetric bubble. The first model and technique are applied at the low-speed stage of expansion and compression of bubbles where their hydrodynamic interaction is significant. The second ones are used at the final high-speed stage of their collapse where the interaction is inessential. The simplest case of the streamer comprising three bubbles is considered as an example to illustrate the features of the developed model and numerical technique. It is shown that under the strong expansion and collapse of an initially spherical cavitation bubble, the presence of neighboring bubbles can substantially deflect the bubble cavity vapor dynamics from what is realized inside a similar but single bubble.
cavitation bubble,
hydrodynamic interaction of bubbles,
shock waves,
deformation of bubbles
Purpose. Numerical simulation of dynamics of bubbles in the central region of a streamer under their strong expansion and collapse with taking into account their interaction and strong non-uniformity of the bubble contents in the final stage of the bubble collapse.
Methodology. The model and the numerical technique are essentially an effective combination of the models and the methods previously created by the authors for calculating the dynamics of interacting weakly-non-spherical bubbles in a streamer and the dynamics of a single axisymmetric bubble.
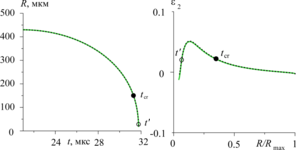
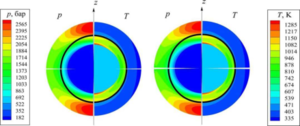
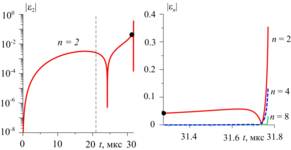
At the low-speed stage of expansion and collapse the hydrodynamic interaction between the bubbles significantly influences the evolution of their shape, whereas the bubbles remain nearly homobaric and their deformations keep small. At this stage, a model of the dynamics of weakly-non-spherical bubbles is used. In the final high-speed stage of the bubble collapse, the interaction between the bubbles is inessential. However, it is necessary to take into account the liquid compressibility, the non-uniformity of the vapor in the bubbles, the formation of radially convergent non-spherical shock waves inside the bubbles. Taking this into account, the model of the dynamics of a single axisymmetric bubble is applied in this stage.
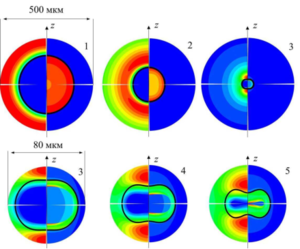
Findings. A mathematical model and an effective numerical technique for study of strong expansion and collapse of cavitation bubbles located in the central region of a streamer where the bubbles are almost motionless are developed. The features of the model and the technique are illustrated by an example of calculating the dynamics of the central bubble in a streamer comprising three bubbles. It is shown that under the strong expansion and collapse of an initially spherical cavitation bubble the presence of the neighboring bubbles can substantially deflect the dynamics of the vapor in its cavity from what is realized inside a similar single bubble.
Originality/value. The proposed mathematical model and numerical technique can be used for studying the properties of the bubble dynamics in the central region of streamers.