ISSN 2658–5782
DOI 10.21662
DOI 10.21662
Electronic Scientific Journal
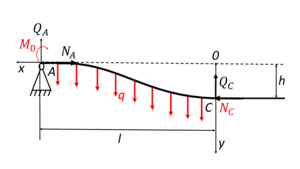
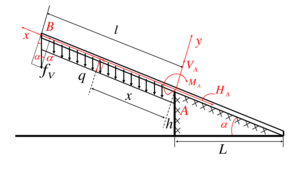
In this article, the process of overcoming the stony obstacle while dragging pipeline through the channel is considered. Depending on the size of the duct and the pipeline itself the permissible size of the obstacle that the pipeline can overcome without resting against the upper part of the channel, is considered. To solve this problem, the pipeline is conditionally divided into two sections: the site located up to the obstacle and resting on it, and a free area that is after the obstacle. Directly on the process of dragging through an obstacle are acting the forces and moments which have influence on the pipeline. Starting from the equations of moment equilibrium for different points of the pipeline, and also from the equations of bending beams the value of the obstacle is evaluated.
pipeline,
pipeline pulling,
underground communications,
mathematical modeling
Purpose: depending on the size of the canal, pipeline and applied tractive effort determine the maximum allowable size of the obstacle.
Methodology: The forces and moments directly influencing the process of overcoming the obstacle are considered. As a condition for overcoming, the condition of parallelity of the free end of the pipeline and the channel axis is used. The length of the free section of the pipeline, necessary for its sufficient bending under its own weight, is estimated. This estimate is obtained from the equations of equilibrium for forces and moments, as well as the differential equation for the bending of a beam. Further, the obtained value is compared with an obvious geometric constraint.
Findings: A method for determining the maximum allowable size of the obstacles has been developed and calculations have been performed for several different parameter values.
Value: For each value of the pipeline parameters, the maximum permissible size of a stony obstacle can be estimated. The relationship between these parameters and the size of the obstacle is clearly nonlinear.
