Davletshin A.I., Khalitova T.F.
Numerical simulation of single vapor bubble dynamics in a liquid in an intense acoustic field.
Multiphase Systems. 13 (2018) 4. 127–135.
Numerical simulation of single vapor bubble dynamics in a liquid in an intense acoustic field
Davletshin A.I., Khalitova T.F.
Institute of Mechanics and Engineering, Kazan Scientific Center of the RAS, Kazan
Abstract
The possibility of increasing the calculation efficiency by the joint use of two models of the dynamics of a single
weakly-nonspherical vapor bubble under its strong collapse in liquid is studied. In both models the motion of
liquid and vapor is split into a spherical component and its small nonspherical perturbation. The models differ
in the description of the spherical component. In the first (simplified) model, it is described by a system of ODE
together with partial differential equations in temperature, derived under the assumption of weak compressibility of
liquid and bubble homobaricity. In the second model, one-dimensional gas dynamics equations are applied. The
advantage of the simplified model consists in determining a numerical solution with much-less computer time costs
in comparison with what is required for the numerical integration of gas dynamics equations. The assumptions used
in the simplified model in the final stage of collapse become incorrect, and, as a result, the numerical solution errors
increase. Therefore, the simplified model is applied at the beginning of bubble collapse, whereas the gas dynamics
equations are used at its end. Within this approach, the numerical solution in the final stage of collapse is dependent
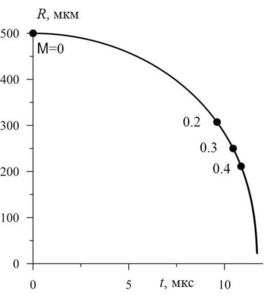
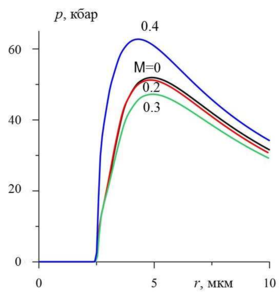
on the moment of transition to the gas dynamics equations. It is shown that satisfactory description of evolution of
bubble sphericity distortion is achieved when the transition is made under the condition that the Mach number M of
vapor in the vicinity of the bubble surface is less than 0.4. Satisfactory resolution of the shock wave in the bubble is
attained when the transition is performed at M<0.2.
Keywordsvapor bubble collapse,
shock waves,
small nonsphericity of bubble
Article outline
Purpose: Improving the efficiency of calculations of single weakly nonspherical vapor bubble dynamics in liquid in an intense acoustic field by jointly applying different models. Investigation of applicability of such models.
Methodology: The model and numerical technique is an effective combination of two models and techniques of calculatinng the dynamics of a weakly-nonspherical bubble, in which the liquid and vapor motion is split into a spherical component and its small non-spherical perturbation. To describe the spherical component of bubble dynamics at the beginning of bubble collapse, a simplified model is used, in which the ODE system is solved together with two heat-conduction equations, whereas gas dynamics equations are applied at the end of collapse. Effects of viscosity, surface tension, evaporation and condensation at the interface are taken into account. The variation of a small non-spherical perturbation of the bubble surface is described by an ordinary second-order differential equation.
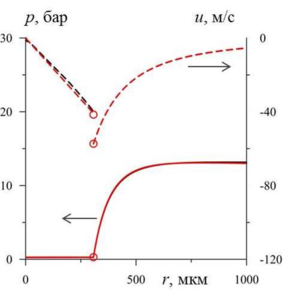
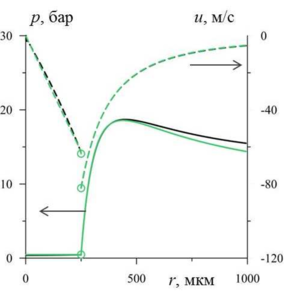
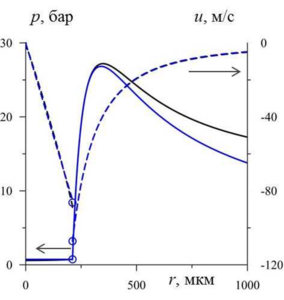
Findings: The errors of using a simplified model in the initial stage of vapor bubble collapse in an intense acoustic field have been studied in order to identify opportunities for improving the efficiency of calculations. It is shown that the simplified modeling with satisfactory error in resolving the radial convergence of shock waves can be applied until the Mach number of the vapor on the bubble surface is less than 0.2, whereas a satisfactory description of the growth in the bubble non-sphericity amplitude is achieved using the simplified modeling until the Mach number is less than 0.4. With the use of the simplified model, the computer time costs are reduced by 3 and 5 times, respectively.
Originality/value: The use of a simplified model of dynamics of a single weakly-nonspherical vapor bubble in liquid makes it possible to increase the calculations efficiency by several times. This can be used in studying the growth of small perturbations of the sphericity of a single vapor bubble in an intense acoustic field.
References
- Lauterborn W., Kurz T. Physics of bubble oscillations // Rep. Prog. Phys. 2010. V. 73. 106501.
(DOI: 10.1088/0034-4885/73/10/106501)
- Ohl S.-W., Klaseboer E., Khoo BC. Bubbles with shock waves and ultrasound: a review // Interface Focus. 2015. V. 5, No 5. 20150019.
(DOI: 10.1098/rsfs.2015.0019)
- Gaitan D.F., Crum L.A. Observation of sonoluminescence from a singl, stable cavitation bubble in a water/glycerine mixture //
12th Intern. Symp. On Nonl. Acoustics. New York: Elsevier. 1990. P. 459–463.
- Storey B.D., Szeri A.J. Water vapour, sonoluminescence and sonochemistry // Proc. R. Soc. Lond. A. 2000. V. 456. P. 1685–1709.
(DOI: 10.1098/rspa.2000.0582)
- Аганин А.А., Ильгамов М.А., Топорков Д.Ю. Зависимость сжатия пара в кавитационных пузырьках в воде и ацетоне от давления жидкости //
Вестник Башкирского университета. 2015. Т. 20, No 3. С. 807–812.
(http://bulletin-bsu.com/arch/files/2015/3/05_4892_Aganin_2v_807-812.pdf)
- Аганин А.А., Халитова Т.Ф. Сильное сжатие среды в сфероидальном кавитационном пузырьке // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2015. Т. 157, No 1. C. 91-–100.
(http://mi.mathnet.ru/uzku1296)
- Топорков Д.Ю. Коллапс слабонесферического кавитационного пузырька в ацетоне и тетрадекане // Многофазные системы. 2018. Т. 13, No 3. С. 23–28.
(DOI: 10.21662/mfs2018.3.003)
- Brenner M.P. Single-bubble sonoluminescence // Rev. Mod. Phys. 2002. V. 74. P. 425–484.
(DOI: 10.1103/RevModPhys.74.425)
- Нигматулин Р.И., Аганин А.А., Ильгамов М.А., Топорков Д.Ю. Эволюция возмущений сферичности парового пузырька при его сверхсжатии // ПМТФ 2014. Т. 55, No 3. С. 82—102.
(DOI: 10.1134/S0021894414030080)
- Nigmatulin R.I., Akhatov I.Sh., Topolnikov A.S. et. al. The theory of supercompression of vapor bubbles and nano-scale thermonuclear fusion //
Phys. Fluids. 2005. V. 17, No 10. P. 1–31.
(DOI: 10.1063/1.2104556)
- Аганин A. A., Халитова Т. Ф., Хисматуллина Н. А. Численное моделирование радиально сходящихся ударных волн в полости пузырька // Матем. моделирование. 2014. Т. 26, No 4. C. 3—20.
(DOI: 10.1134/S2070048214060027)
- Plesset M.S. The dynamics of cavitation bubbles // J. Appl. Mech. 1949. P. 277–282.
- Akhatov I., Lindau O. et. al. Collapse and rebound of a laser-induced cavitation bubble // Phys. Fluids. 2001. Т. 13, No 10. С. 2805–2819.
(DOI: 10.1063/1.1401810)
- Аганин А.А., Ильгамов М.А. и др. Динамика пузырька газа в центре сферического объема жидкости // Математическое моделирование. 2001. Т. 13, No 1. С. 26–40.
(http://mi.mathnet.ru/mm664)
- Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния органических жидкостей на примере ацетона // ДАН. 2007. Т. 415, No 5. С. 617–621.
(https://elibrary.ru/item.asp?id=9533722)
- Аганин А.А., Халитова Т.Ф., Хисматуллина Н.А. Расчет сильного сжатия сферического парового пузырька в жидкости // Вычислительные технологии. 2008. Т. 13, No 6. С. 17–27.
(http://www.ict.nsc.ru/jct/content/t13n6/aganin.pdf)
- Аганин А.А., Халитова Т.Ф. Зависимость образования ударной волны в кавитационном пузырьке от температуры жидкости //
Труды Института механики им. Р.Р. Мавлютова Уфимского научного центра РАН. 2017. Т. 12, No 1. C. 89–94.
(DOI: 10.21662/uim2017.1.013)