Article outline

In the work investigated the flexural vibrations of the pipeline. The pipeline has a free sagging section. Parts of the pipeline on both sides of the sagging section have elastic supports. It is assumed that a constant longitudinal force acts along the neutral line. The influence of internal pressure in the pipe on bending vibrations is taken into account. The influence of the velocity of the transported liquid on the oscillations is also taken into account. The direct problem of determining the natural frequencies of flexural vibrations of the pipeline depending on the fluid pressure, the elasticity of the supports, the velocity of the liquid flow through the pipe is solved. The equation of flexural vibrations of the pipeline according to the Kirchhoff model is used. The characteristic equation is solved by the Ferrari method. According to this method, the resolvent of the basic equation is written, which is solved by one of the numerical methods or the Cardano method. Then the general solution is recorded. Substituting the General solution in the boundary conditions, we obtain a system of equations. This system gives a frequency equation, which is solved numerically.

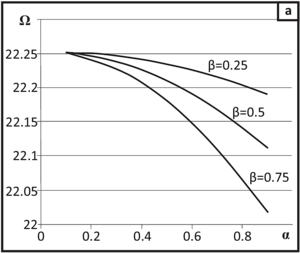
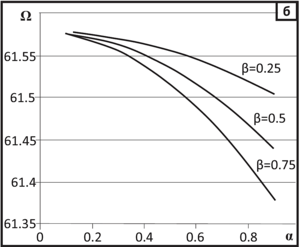
Particular and limiting cases are considered, for example, when the stiffness of the supports is very large, the pipeline oscillates as a pipeline with rigidly fixid ends. Another limiting case is when the stiffness of the supports is infinitely small. This corresponds to the fluctuations of the pipeline with the fixing of the «free end – free end» type. The frequency equation here takes the same form as in the case of a pipeline with rigidly fixed ends. Also, a special case is given when the velocity of the transported liquid is zero. In this case, a simple frequency equation known in the literature is obtained. The calculation results of natural frequencies are shown in tables. The graphs of the dependence of the first and second eigenfrequencies of flexural vibrations of the freely sagging part of the pipeline on the velocity of the transported liquid at different values of the liquid density parameter are constructed. The eigenfrequencies of the pipeline oscillations as a solid body on elastic supports with zero wavenumber or wavelength equal to infinity are given. In the mathematical package Maple the program code for numerical calculation of eigenfrequencies of flexural vibrations of the pipeline is developed.

It is shown that with the growth of the velocity parameter there is a decrease in the natural frequencies of flexural vibrations of the pipeline, and the faster the higher the density parameter of the liquid. It is determined that with an increase in the mass of the liquid per unit length of the pipeline there is a decrease in the natural frequencies of bending vibrations of the pipe. It is found that with the increase in the mass flow through the pipe, the natural frequencies of bending oscillations also decrease. It is confirmed that the frequencies of flexural vibrations of the pipeline are the same for the cases of pipe fastening «rigid fixing – rigid fixing» and «free end – free end».

The results of the study will contribute to the development of methods of acoustic diagnostics and non-destructive testing methods and can find technical application for monitoring and diagnostics of pipeline systems.