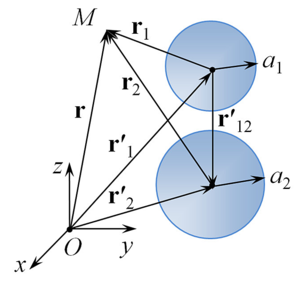
A mathematical model extension is presented and numerical studies were made for the problem of acoustic scattering from two soundproof spheres (the case of hard spheres) with an arbitrary acoustic impedance under the action a spherical wave from a monopole radiation source arbitrarily located in space. The case of two spheres is of practical interest, since, on the one hand, the scattered fields from the spheres interact with each other, and on the other hand, the interaction is simple enough for it to be studied in detail. When solving the Helmholtz equations, a numerical technique based on the fast multipole method is used, which allows to achieve high accuracy of the results obtained with minimal computer time. The testing of the algorithm was carried out on the basis of the known data (from the literature) of the response on the surface of one of the spheres in the case when the axis connecting the monopole radiation source and the center of the first sphere is perpendicular to the axis connecting the centers of the two spheres. The pressure distribution around the spheres is investigated for different values of the distance between the centers of the spheres and the arbitrary location of the monopole radiation source in space. It is shown that with certain parameters of the system, the presence of a second sphere can lead to the appearance of an increase or decrease zone of pressure. The obtained results will further allow generalizations of the mathematical model to the cases of acoustic scattering from a pair of sound-permeable spheres (cases of gas bubbles or liquid droplets) and many spheres (both coaxially and arbitrarily arranged in space), and can also be used for test calculations during verification numerical solution of these generalized problems.
acoustic scattering,
soundproof sphere,
monopole radiation source,
acoustic impedance
When an acoustic wave interacts with obstacles, additional (scattered) waves appear that propagate in all directions from the obstacles. This phenomenon is called scattering (diffraction) of sound. Its study is one of the important problems of acoustics, because it is based on many of the practical application of acoustic waves, such as sonar, non-destructive testing equipment, medical scanners, sensing of the atmosphere and ocean, etc. One of the actual sub-tasks is to study the acoustic scattering spheres sets, including solid spheres, under various external influences.
In the paper a mathematical model extension is presented and numerical studies were made for the problem of acoustic scattering from two soundproof spheres (the wave inside the sphere does not pass – the case of solid spheres) with an arbitrary acoustic impedance under the action a spherical wave from a monopole radiation source arbitrarily located in space.
The case of two spheres is of practical interest, since, on the one hand, the scattered fields from the spheres interact with each other, and on the other hand, the interaction is simple enough for it to be studied in detail.
Problem: generalization of the numerical model for determining the field around a pair of soundproof spheres with an arbitrary acoustic impedance when a spherical wave is incident from a monopole radiation source that is arbitrarily located in space.
Methods: When solving the Helmholtz equations, a numerical technique based on the fast multipole method is used. This calculation technique allows to achieve high accuracy of the results obtained with minimal expenditure of computer time. The problem is considered in axisymmetric formulation. As a result of numerical modeling, program codes were written in the Fortran 90 language.
The following numerical studies were made:
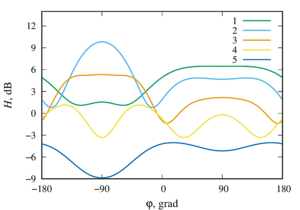
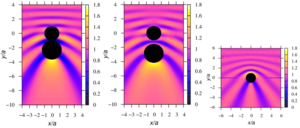
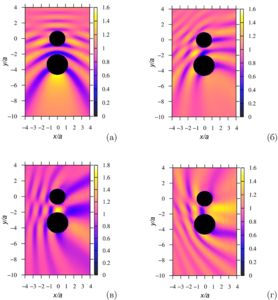
As a result of the research, it has been determined that with certain system parameters of the system,the presence of a second sphere can lead to the appearance of a increase or decrease zone of pressure.
It is planned to carry out a detailed parametric analysis for a wider range of parameters, as well as for different spheres of radii, values of acoustic impedance and physical properties of the environment, etc. The numerical model obtained in this work will also allow generalizations of the mathematical model to the cases of acoustic scattering from a pair of sound-permeable spheres (cases of gas bubbles or liquid droplets) and many spheres (both coaxially and arbitrarily arranged in space), and obtained results can be used for test calculations during verification numerical solution of these generalized problems.