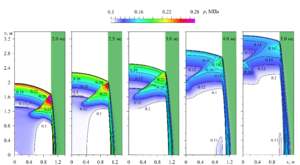
The numerical study of the powerful air spherical shock-wave pulse interaction with the protective aqueous foam barrier with the initial liquid volume fraction of 0.2 is carried out. The foam layer thickness is selected to satisfy the condition of the non-reflection of compression wave from the foam external boundary at the considered time intervals. In studying the wave flows dynamics, we used the assumption of the foam structure destruction into the microdrops suspension behind the strong shock wave front. The two-phase medium is described on the basis of the gas-droplet mixture model, which includes the laws of conservation of mass, momentum and energy for each phase in accordance with the single-pressure, two-speed, two-temperature approximations in a two-dimensional axisymmetric formulation. The Schiller–Naumann model is used for taking into account the interfacial drag forces. The contact heat transfer influence at the interface between the phases is taken into account by the Ranz–Marshall model. To describe the properties of air and water, the Peng–Robinson and perfect fluid equations of state are used. The numerical implementation of the model is carried out using the OpenFOAM open-source software with the two-step PIMPLE algorithm. The numerical study results are presented as spatial distributions of pressure fields, velocities and streamlines. The significant attenuation of the spherical shock wave intensity during its interaction with the aqueous foam layer has been established. The causes and dynamics of the toroidal vortices series formation in the gas region behind the shock front are investigated. The results reliability is confirmed by comparison with the solutions of the similar problem, found by another numerical method.
spherical shock wave,
shock impulse,
aqueous foam barrier,
OpenFOAM package,
numerical modeling,
vortex flows
Purpose. Investigation of the spherical air shock pulse interaction process with the aqueous foam barrier.
Methodology. The two-phase model of gas-liquid mixture in a two-dimensional axisymmetric formulation in the single-pressure, two-speed, and two-temperature approximations is developed. It is assumed, that behind the front of the strong shock wave, the foam is being destroyed into monodisperse microdroplets, this allows using the gas-droplet model in its description. The system of model equations includes the laws of conservation of mass, momentum and energy for each phase, taking into account the interfacial drag force according to the Schiller-Naumann model and contact interfacial heat transfer stated by the Ranz-Marshall model. The properties of gas and water are described by the Peng-Robinson and perfect fluid equations of state. The numerical implementation of the model was carried out using the OpenFOAM open-source software, in which the system of equations was discretized using the finite volume method. The solution method is based on the two-step algorithm PIMPLE.
Findings. The cylindrical region filled with gas and containing the aqueous foam layer with the liquid volume fraction of 0.2 is considered. The foam layer thickness is selected to satisfy the condition of the non-reflection of compression wave from the foam external boundary at the considered time intervals. At the initial moment of time, the pressure pulse with the maximum amplitude of 100 MPa is set in the center of the computational domain and approximated by the smooth exponential function. The numerical modeling results of the task showed that spherical shock wave interaction with the foam layer causes the foam compression, which is accompanied by the increase in liquid volume fraction and the significant decrease in the propagation velocity of the compression wave front, passing into the foam layer. In this case, foam, as a denser medium, reflects the wave impulse to the gas region and prevents the shock wave propagation deep into the aqueous foam barrier.
Calculations visualization demonstrates the appearance of large vortex structures of toroidal shape behind the shock wave front. Further evolution of the process leads to the flux turbulization and the shift of intense vortex flow region in the direction of the shock wave front motion. The obtained results reliability is confirmed by satisfactory agreement with the solutions of the similar problem found using the method of movable Lagrangian grids. The main reason for the formation of vortex structures behind the shock wave front is the streamlines curvature due to the development of Richtmyer – Meshkov instability resulting from the bending of the gas-foam interface during its interaction with a spherical shock wave.
Value. The numerical simulation of the air spherical shock pulse interaction process with the aqueous foam barrier has been carried out. The gas-liquid mixture model was used in the work, taking into account the interfacial interaction forces and heat transfer processes on the contact interface. To describe the properties of air and water, the Peng-Robinson and perfect fluid equations of state were used. The numerical solution of the problem was carried out in a two-dimensional axisymmetric approximation using the OpenFOAM package. The reliability of the obtained solutions was confirmed by comparison with the solutions of the similar problem by other numerical methods and experimental data. The numerical results analysis showed, that the increase in the liquid volume fraction of the foam layer, compacted under the influence of the shock pulse, leads to decrease in the shock wave front velocity and blocks its passage into the foam. The detailed analysis of the causes of occurrence, evolution of the toroidal vortices series and flow turbulization in the gas region behind the shock wave front has been carried out.