ISSN 2658–5782
DOI 10.21662
Electronic Scientific Journal


© Институт механики
им. Р.Р. Мавлютова
УФИЦ РАН

Яндекс.Метрика web site traffic statistics

Minibaev M.R., Mikhaylenko C.I. Investigation of the influence of boundary conditions in the numerical solution of a vortex tube model . Multiphase Systems. 14 (2019) 2. 89–100 (in Russian).
2019. Vol. 14. Issue 2, Pp. 89–100
URL: http://mfs.uimech.org/mfs2019.2.013,en
DOI: 10.21662/mfs2019.2.013
Investigation of the influence of boundary conditions in the numerical solution of a vortex tube model
Minibaev M.R.∗,∗∗, Mikhaylenko C.I.∗∗
∗Ufa State Aviation Technical University, Ufa, Russia
∗∗Mavlyutov Institute of Mechanics, UFRC of RAS, Ufa, Russia

Abstract

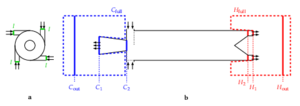
The applicability of various boundary conditions in the computational simulation of a Ranque–Hilsch vortex tube is investigated. A review of existing works on the effect of geometry and various thermodynamic parameters on the efficiency of the pipe is made. The substantiation of the possibility of introducing additional computational domains when moving the boundaries to study the influence of boundary conditions when modeling gas dynamics problems is given. To simulate the dynamics of a gas in a vortex tube, a mathematical model is written that includes the Navier–Stokes system of equations describing a compressible viscous fluid, which is closed by the equation of state of an ideal gas. Existing methods for calculating turbulent flows are considered. The applicability of various semi-empirical models of turbulence for modeling a vortex tube is described. The possibility of using the selected k−ε model and its description is argued. 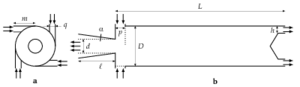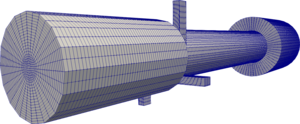The boundary conditions characteristic of the vortex tube model are described, and the boundary conditions most combined in the simulation of gas dynamics problems are also shown. Presents a grid that takes into account the area formed by the removal of boundaries. The solution is based on the sonicFoam algorithm in the OpenFOAM package. 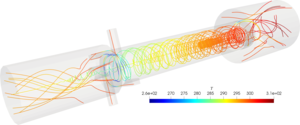Utilities of the postprocessor are used when preparing the model for calculations on a high-performance cluster and utilities for averaging the obtained physical quantities. The simulation results for different combinations of boundary conditions and models with remote boundaries are given. Comparison of the results obtained. It is shown that the geometrical dimensions have a strong influence on the operation of the pipe; the correct choice of boundary conditions makes it possible to obtain the values of physical quantities that are closest to the known experimental ones. Moving the boundaries away from direct exits provides an opportunity to more accurately estimate the effects that arise near the real boundaries of the vortex tube, especially affecting the magnitude of the Ranque–Hilsch effect.

Keywords

vortex tube,
boundary conditions,
CFD,
turbunece,
OpenFOAM

Article outline

Objective: to study the influence of boundary conditions in the numerical solution of a vortex tube model.

Research methods: to model gas dynamics in a vortex tube, a mathematical model was used that includes the Navier-Stokes system of equations describing a compressible viscous fluid that is closed by the equation of state of an ideal gas. To simulate turbulence, a standard k-ε model was used. The solution is carried out according to the sonicFoam algorithm in the OpenFOAM package.

During the study, the following results were obtained:

  1. The applicability of various boundary boundary conditions in the computational modeling of the Rank-Hills vortex tube is investigated.
  2. The substantiation of the possibility of introducing additional computational domains when moving the boundaries to study the influence of boundary conditions when modeling gas dynamics problems is given.
  3. Existing methods for calculating turbulent flows are considered. The applicability of various semi-empirical turbulence models for modeling a vortex tube is described. The possibility of using the selected k-ε model is substantiated and its description is given.
  4. The boundary conditions characteristic of the vortex tube model are described, and the boundary conditions that are most compatible when modeling gas dynamics problems are also shown.
  5. A mesh is modeled that takes into account the areas that form when borders are removed.
  6. The simulation results for different combinations of boundary conditions and models with remote boundaries are presented.

It is shown that the geometric dimensions have a strong influence on the operation of the pipe, the correct choice of boundary conditions allows us to obtain the values of physical quantities that are closest to the known experimental ones. Moving the boundaries from the immediate exits provides an opportunity to more accurately assess the effects that arise near the real boundaries of the vortex tube, especially affecting the magnitude of the Rank – Hills effect.

Thus, in the course of the work, conclusions were drawn about the importance of the correct choice of boundary conditions in the mathematical modeling of temperature separation processes in the channel of the Rank-Hills pipe. This is due to the fact that any boundary conditions inevitably affect the result within the computational domain.

It was shown in the work that the introduction of additional areas near the hot and cold exits from the vortex tube (pushing the boundary ”to infinity“) leads to a change in the average value of the main physical quantities directly at the exits and near them inside the pipe channel.

The presented results allow us to conclude that it is necessary to use the additional areas described above in vortex tube models, despite the significant increase in machine resources.

Further work involves the search for such boundary conditions that will make it possible to bring the boundary of the computational domain closer to the exits from the vortex tube without introducing a large error into the result.

References

  1. Ranque G.J. Experiments on expantion a vortex with Simultaneous Exhaust of hot air and cold air // J. Phys. Radium. 1933. V. 4. Pp. 112–114 (in French).
  2. Hilsch R. The Use of the Expansion of Gases in a Centrifugal Field as Cooling Process // Review of Scientific Instruments. 1947. V. 18. Pp. 108–113.
    DOI: 10.1063/1.1740893
  3. Khodorkov L., Poshernev N.V., Zhidkov M.A. The vortex tube — a universal device for heating, cooling, cleaning, and drying gases and separating gas mixtures // Chemical and Petroleum Engineering. 2003. V. 39, No. 7–8. Pp. 409–415.
    DOI: 10.1023/A:1026336813155
  4. Exair.com. Vortex Tubes.
    URL: http://www.exair.com/index.php/products/vortex-tubes-and-spot-cooling-products/vortex-tubes/vt.html
    (дата обращения: 17.05.2019).
  5. Ebmeier R., Whitney S., Alugupally S., Nelson M., Padhye N., Gogos G., Viljoen H.J. Ranque–Hilsch Vortex Tube Thermocycler for DNA Amplification // Instrumentation Science & Technology. 2004. V. 32. Pp. 567–570.
    DOI: 10.1081/CI-200029810
  6. Boucher R.F., Tippetts J.R. Vortex-tube-driven thermo-electricity // In Sixth triennal international symposium on Fluid Control, Measurement and Visualization, 6th, Sherbrooke, Canada. 2000. Paper 50.
  7. Westley R. A Bibliography and Survey of The Vortex Tube. The College of Aeronautics. 1957. P. 38.
  8. Vortex Tubes, CNC Coolers, Cool Tool and Compressed Air Products.
    URL: https://arizonavortex.com/vortex-tubes/
    (дата обращения: 27.12.2018)
  9. Akhmetov Yu.M., Zhernakov V.S., Tselischev A.V. [Investigation of the process of separation of gas-liquid flow in a vortex tube] Issledovanie processa separacii gazozhidkostnogo potoka v vixrevoj trube // [USATU Bulletin] Vestnik UGATU. 2011. V. 15, No. 4(44). Pp. 120–126 (in Russian).
    http://journal.ugatu.ac.ru/index.php/Vestnik/article/view/812
  10. Baz A., Gilheany J., Kalvitas A. Feasibility of vortex tube assisted environmental control of an underwater research habitat // Ocean Eng. 1987. V. 15, No. 1. Pp. 34–54.
    DOI: 10.1016/0029-8018(88)90018-2
  11. Bruno T.J. Laboratory applications of the vortex tube // Journal of Chemical Education. 1987. V. 64. Pp. 987–988.
    DOI: 10.1021/ed064p987
  12. Gutsol A.F. The Ranque effect // Physics-Uspekhi. 1997. V. 40. Pp. 639–658.
    DOI: 10.1070/PU1997v040n06ABEH000248
  13. Eiamsa-Ard S., Promvonge P. Review of Ranque-Hilsch effects on vortex tubes // Renewable and Sustainable Energy Reviews. 2008. V. 1. Pp. 1822–1842.
    DOI: 10.1016/j.rser.2007.03.006
  14. Attalla M., Ahmed H., Ahmed M.S., El-Wafa A.A. An experimental study of nozzle number on Ranque–Hilsch counter-flow vortex tube // Experimental Thermal and Fluid Science. 2017. V. 82. Pp. 381–389.
    DOI: 10.1016/j.expthermflusci.2016.11.034
  15. Hamdan M.O., Al-Omari S.-A., Oweimer A.S. Experimental study of vortex tube energy separation under different tube design // Experimental Thermal and Fluid Science. 2018. V. 91. Pp. 306–311.
    DOI: 10.1016/j.expthermflusci.2017.10.034
  16. Majidi D., Alighardashi Н., Farhadi F. Best vortex tube cascade for highest thermal separation // International Journal of Refrigeration. 2017. V. 85. Pp. 282–291.
    DOI: 10.1016/j.ijrefrig.2017.10.006
  17. Volkov K.N., Emel’yanov V.N., Zazimko V.A. [Turbulent jets — statistical models and modeling of large eddies] Turbulentnye strui — sttisticheskie modeli i modelirovanie kruphyx vixrej. M: FIZMATLIT. 2014. P. 360 (in Russian).
  18. Marin D.F., Mikhaylenko C.I., Khaziev L.Kh. [Direct numerical simulation of Rankque effect] Pryamoe chislennoe modelirovanie e’ffekta Ranka // Parallel numerical techniques: proceedings of international conference PaVT’2011. Pp. 539–547 (in Russian).
    http://omega.sp.susu.ru/books/conference/PaVT2011/short/197.pdf
  19. Marin D.F., Mikhaylenko C.I. [Numerical investigation of the mechanism of the Ranque-Hilsch effect in the vortex tube channel] Chislennoe issledovanie mexanizma vozniknoveniya e’ffekta Ranka–Xilsha v kanale vixrevoj truby // Vestnik of Lobachevsky University of Nizhni Novgorod. 2011. No. 4–3. P. 977 (in Russian).
  20. Gazizov R.K., Lukashuk S.Yu., Mikhaylenko C.I. [Development of parallel technique based on the principle of spatial decomposition for solving problems of continuum mechanics]. Vestnik Ufimskogo gosudarstvennogo aviacionnogo nexnucheskogo universiteta [Ufa state aviation technical university Bulletin]. 2013. V. 4, No. 1. Pp. 100–107 (in Russian)
  21. Moiseeva E., Mikhaylenko C., Malyshev V., Maryin D., Gumerov N. FMM/GPU accelerated molecular dynamics simulation of phase transitions in water-nitrogen-metal systems // ASME International Mechanical Engineering Congress and Exposition, Proceedings, IMECE 2012. 2012. Pp. 883–892.
    https://www.tib.eu/en/search/id/BLCP:CN084513203/IMECE2012-86246-FMM-GPU-Accelerated-Molecular-Dynamics/
  22. Noskov A.S., Lovtsov A.V., Khait A.V. Simulation of gas flow in double-circuit Ranque–Hilsch vortex tube // Computational Continuum Mechanics. 2012, V. 5. No 3. Pp. 313–321 (in Rusian).
    DOI: 10.7242/1999-6691/2012.5.3.37
  23. Khait A., Noskov A., Alekhin V., Antipin A. Numerical simulation and visualization of air flow in Rnque–Hilsch vortex tube // Proceedings of the 13th International Conference on Construction Applications of Virtual Reality, 30-31 October 2013, London, UK. 2013. Pp. 638–648.
    DOI: 10.13140/RG.2.1.2916.2089
  24. Common Combinations Pressure-velocity systems.
    URL: https://www.openfoam.com/documentation/guides/latest/doc/guide-bcs-common-combinations.html
    (дата обращения: 27.05.2019).
  25. Mikhaylenko C.I. Simulation of the vortex tube: design of a hexagonal mesh for computational experiments in OpenFOAM // Proceedings of the Mavlyutov Institute of Mechanics. 2016. V. 11, No. 1. Pp. 112–118 (in Russian).
    DOI: 10.21662/uim2016.1.017
  26. Jang D.S., Jetli R., Acharya S. Comparison of the PISO, SIMPLER, and SIMPLEC algorithms for the treatmentof the pressurevelocity coupling in steady fow problems // Numer. Heat Transfer Appl. 1986. V. 10. Pp. 209–228.
    DOI: 10.1080/10407788608913517
  27. Borisoglebskiy I.K., Metusova M.V., Mikhaylenko C.I. The dependence of the Ranque–Hilsch effect on the cold outlet geometry // Multiphase Systems. 2018. V. 13, No. 3. Pp. 52–58 (in Russian).
    DOI: 10.21662/mfs2018.3.008