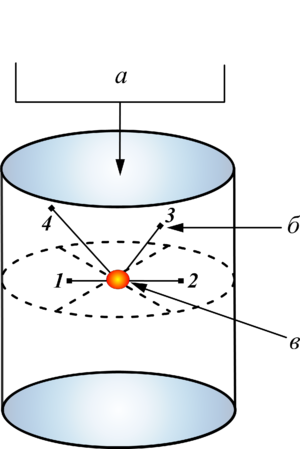
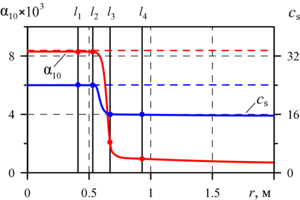
The two-phase model of dry aqueous foam dynamic behavior under the strong shock wave influence is presented under assumption that the foam structure under shock loading is destroyed into a suspension of monodispersed microdrops with the formation of a gas-droplet mixture. The system of equations for the model of aqueous foam includes the laws of conservation of mass, momentum and energy for each phase in accordance with the single-pressure, two-speed, two-temperature approximations in a three-dimensional formulation, taking into account the Schiller–Naumann interfacial drag force and the Ranz–Marshall interfacial contact heat transfer. The thermodynamic properties of air and water forming a gas-droplet mixture are described by the Peng–Robinson and Mie–Grueneisen equations of state. The presence of non-uniform process in height of aqueous foam syneresis, which is due to gravitational forces, is taken into account by setting the distribution of the liquid volume fraction in the foam. An additional consideration of the syneresis process during calculating the intensity of interphase drag forces according to the Schiller–Naumann model was controlled by introducing the parameter depending on the spatial distribution of the initial liquid volume fraction of the foam. The spherical explosion is modeled in the form of the shock wave pulse whose energy coincided with the charge energy of the HE used in the experiments. The problem numerical solution is implemented using the OpenFOAM free software package based on the two-step PIMPLE computational algorithm. The numerical solution of the problem, obtained on the basis of the proposed gas-droplet mixture model, is in satisfactory agreement with the experimental data on a spherical explosion in aqueous foam. The analysis of the spherical shock wave dynamics while its propagation through aqueous foam is given. The causes of the significant decrease in the amplitude and velocity shock waves propagation in the medium under study are investigated.
spherical shock wave,
aqueous foam,
OpenFOAM package,
numerical modeling
Purpose. Investigation of dynamics a spherical shock wave propagation in dry aqueous foam, taking into account the influence of interfacial drag forces, contact heat transfer and foam syneresis process.
Methodology. The two-phase model of gas-liquid mixture in the two-dimensional axisymmetric formulation under the conditions of single-pressure, two-speed, two-temperature approximations is proposed. While describing the behavior of aqueous foam under shock loading, it is assumed that in the process of its interaction with the strong shock wave, the foam structure is being destroyed into monodisperse microdroplets, and model of the gas-droplet mixture is applicable. The system of model equations includes the laws of conservation of mass, momentum and energy for each phase, taking into account the Schiller-Naumann interfacial drag forces and the Ranz-Marshall interphase heat transfer processes. The non-uniformity of foam deposition process is taken into account in the Schiller-Naumann drag model by introducing the parameter that depends on the spatial distribution of the initial liquid volume fraction of the foam. The Peng-Robinson and Mie-Grueneisen equations of state are used to describe the properties of gas and water. The proposed gas-droplet mixture model is implemented in the solver created in OpenFOAM numerical simulation open package. Discretization of the model equations system is carried out by the finite volume method. The two-step computational algorithm PIMPLE is chosen as the solution method.
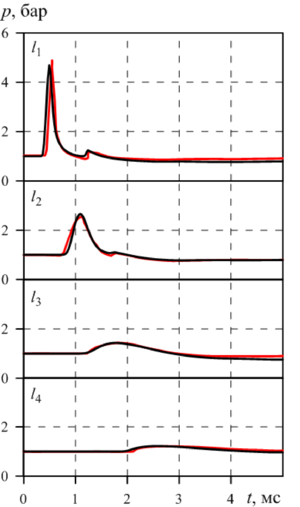
Findings. The numerical simulation of a spherical shock wave evolution is performed under conditions of experiments on the HE explosion in the dry aqueous foam with the initial liquid volume fraction of 0.0083. The spherical region with the radius of 2 m is considered. The explosion is simulated in the center of region at initial time in the form of pressure pulse approximated by the smooth exponential function. The generated shock wave pulse with the maximum amplitude of 3000 MPa has the energy equal to the explosion energy in the experiment under consideration. The numerical modeling results of the task are compared with experimental data obtained from sensors attached at different heights and distances from the explosion center. To account for the foam syneresis process for each of the gauges, a separate problem was solved with the individual initial distribution of liquid fraction in the foam. Both in calculations and in experiments, the shock wave pulse at the short distance from the center of the explosion has two-wave structure, which, as shock wave propagates deep into the foam, is “spread” under the influence of interfacial drag forces and contact heat transfer. The comparative analysis of the calculated and experimental pressure profiles at the locations of the gauges demonstrates their good agreement.
Value. The numerical simulation and study of process of spherical shock wave propagation formed as a result of the HE explosion in aqueous foam was performed for the conditions of the selected experiments. While studying the shock wave dynamics in aqueous foam, the proposed model of the gas-droplet mixture that takes into account the forces of interfacial interaction, contact heat transfer and the effect of the aqueous foam syneresis due to gravitational forces was used. The numerical simulation of the investigated problem is based on the free OpenFOAM package. The comparison of the numerical solutions obtained for the pressure time dependences and experimental pressure oscillograms at the points of the sensors installation showed their good agreement on the velocity of propagation and the amplitude of shock wave pulse. The analysis the causes of shock wave energy dissipation in aqueous foam, leading to its significant attenuation was given.