Agisheva U.O., Vdovenko I.I., Galimzyanov M.N.
The effect of diffusion on the acoustic properties of a bubble fluid. Multiphase Systems. 14 (2019) 3. 165–175 (in Russian).
The effect of diffusion on the acoustic properties of a bubble fluid
Agisheva U.O.∗, Vdovenko I.I.∗∗, Galimzyanov M.N.∗
∗Mavlyutov Institute of Mechanics, UFRC RAS, Ufa
∗∗Birsk branch of the Bashkir State University, Birsk
Abstract
The problems of wave propagation in bubble media have been of great interest to researchers for almost half a century
in connection with the wide distribution of these systems in nature and their intensive use in modern technologies. It
is known from the literature that the intensity of attenuation of sound disturbances in the gas-liquid media under
consideration is mainly determined by the thermophysical characteristics of the gas in the bubbles. It turns out that
these effects are significantly enhanced with increasing vapor concentration due to an increase in the temperature
of the system. There are a large number of publications in the literature in which various statements of the wave
action on bubble media have been considered. In the present work, the propagation of small perturbations in a liquid
with bubbles filled with vapor and a gas insoluble in the liquid phase is considered in the plane one-dimensional
and single-velocity approximations. The rate of liquid evaporation (condensation) inside the bubble was determined
from the condition of heat balance. To take into account interphase heat and mass transfer, the heat conduction and
diffusion equations inside the bubble and the heat conduction equation in the fluid around the bubble are used. From
the condition for the existence of a solution in the form of a decaying traveling wave, taking into account the effects of
acoustic unloading of bubbles, the dispersion equation is written. From the condition for the existence of a solution in
the form of a decaying traveling wave, taking into account the effects of acoustic unloading of bubbles, the dispersion
equation is written. Based on the obtained dispersion equation, relations are written for the equilibrium speed of
sound depending on the thermophysical parameters of the medium and numerical calculations are performed for
water with vapor-gas bubbles. The features of the reflection of harmonic waves from the interface between the
“pure” liquid and liquid with vapor-gas bubbles are studied. The influence of the perturbation frequency and the
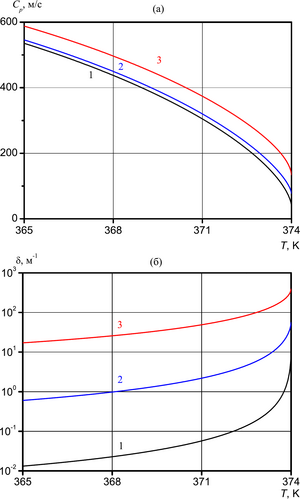
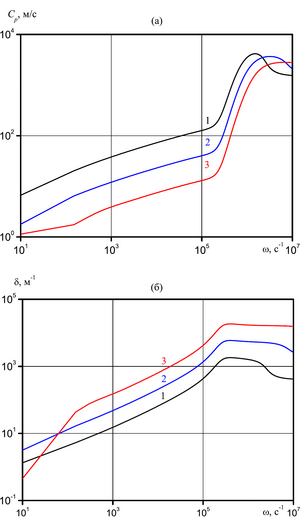
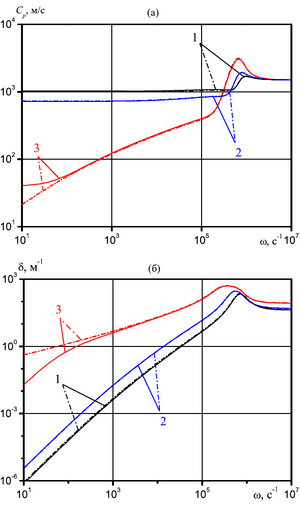
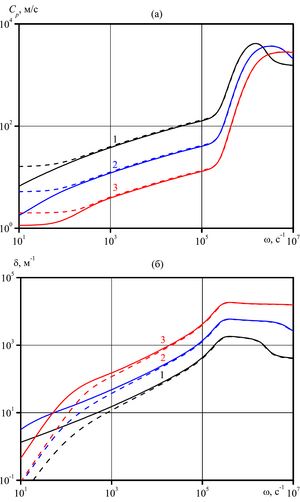
temperature of the medium on the attenuation coefficient of the acoustic wave is studied. The influence of diffusion
on the evolution of harmonic waves is analyzed.
Keywordsacoustic wave,
superheated liquid,
bubbles,
analysis of variance,
phase velocity,
attenuation coefficient,
diffusion
Article outline
Problem: Study of the influence of disturbance frequency and medium temperature on the acoustic wave attenuation coefficient. Analysis of the influence of diffusion on the evolution of harmonic waves.
Methods: From the condition for the existence of a solution in the form of a decaying traveling wave, taking into account the effects of acoustic unloading of bubbles, the dispersion equation is written out, numerical calculations for water with vapor-gas bubbles are performed.
In a study was determined:
The study of harmonic acoustic waves in a liquid with vapor-air bubbles taking into account diffusion showed that for the problems under consideration this accounting can be significant only for superheated liquids in the low-frequency region. This is due to the increasing role of phase transitions due to an increase in the mass concentration of vapor in the bubbles under the action of capillary forces on the interface.
References
- Kutateladze S.S. and Nakoryakov V.E.
[Heat and mass transfer in gas–liquid systems]
Teplomassoobmen i volni v gazojidkostnih sistemah. Novosibirsk: Nauka, 1984. P. 302 (in Russian).
- Nigmatulin R.I.
Dynamics of Multiphase Media.
New York: Hemisphere, 1991, vols. 1 and 2. P. 360 and P. 464.
- Shagapov V.Sh., Lepikhin S.A. and Galimzyanov M.N.
Realization of high pressures and temperatures in the gas phase of a bubble liquid flowing through a nozzle //
Journal of Engineering Physics and Thermophysics. 2007. V. 80, No. 6. Pp. 1206–1209.
DOI: 10.1007/s10891-007-0155-0
- Galimzyanov M.N. and Lepikhin S.A.
Outflow of a two-phase mixture through a nozzle with account for phase transitions //
Vestnik Samarsk. Gos. Univ. Mekh. 2010. No. 2 (76). Pp. 96–104 (in Russian).
https://elibrary.ru/item.asp?id=16059300
- Galimzyanov M.N., Lepikhin S.A. and Chiglintsev I.A.
Propagation of nonlinear waves in channels with variable crosssection, led to the gas hydrate formation //
Vestnik Samarsk. Gos. Univ. Mekh. 2012. No. 3/1(94). Pp. 103–115 (in Russian).
https://elibrary.ru/item.asp?id=18242265
- Bolotnova R.Kh., Galimzianov M.N., Topolnikov A.S. et al.
The hydrodynamic processes in bubbly liquid flowing in tubes and nozzles.
World Acad. Sci. Eng. Technol. 2012. V. 68. Pp. 1992–1999.
DOI: 10.5281/zenodo.1329811
- Nigmatulin R.I., Shagapov V.Sh., Gimaltdinov I.K. et al.
Two-dimensional pressure waves in a liquid containing bubble zones //
Doklady Physics. 2001. V. 46, No. 6. Pp. 445–451.
DOI: 10.1134/1.1384945
- Galimzyanov M.N., Gimaltdinov I.K. and Shagapov V.Sh.
Two-dimensional pressure waves in a fluid with bubbles //
Fluid Dynamics. 2002. V. 37, No. 2. Pp. 294–301.
DOI: 10.1023/A:1015818602291
- Galimzyanov M.N.
Propagation of compression waves in finite-size bubbles zones //
Vestnik Udmurt. Univ. Matematika. Mekhanika. 2010. No. 2. Pp. 57–66 (in Russian).
http://vst.ics.org.ru/journal/article/1677/
- Galimzyanov M.N.
Propagation of Pressure Waves in Finite-Size Bubbles Zones //
Izv. Sarat. Univ. Mathematics. Mechanics. Informatics. 2010. V. 4. Pp. 27–35 (in Russian).
DOI: 10.18500/1816-9791-2010-10-4-27-35
- Bolotnova R.Kh., Galimzianov M.N., Topolnikov A.S. et al.
Nonlinear effects in bubbly liquid with shock waves //
World Acad. Sci. Eng. Technol. 2012. V. 68. Pp. 2000–2007.
DOI: 10.5281/zenodo.1082523
- Bolotnova R.Kh., Galimzyanov M.N. and Agisheva U.O.
Modeling of shock waves in gas–liquid mixtures.
Izv. Vyssh. Uchebn. Zaved. Fiz.-Mat. Nauki. 2011. No. 2. Pp. 3–14 (in Russian).
https://izvuz_fmn.pnzgu.ru/fmn1211
- Agisheva U.O., Bolotnova R.Kh., Buzina V.A. et al.
Parametric analysis of the regimes of shockwave effect on gas–liquid media //
Fluid Dynamics. 2013. Vol. 48, No. 2. Pp. 151–162.
DOI: 10.1134/S0015462813020038
- Hawker N.A. and Ventikos Y.
Interaction of a strong shockwave with a gas bubble in a liquid medium: a numerical study //
Journal of Fluid Mechanics. 2012. V. 701. Pp. 59–97.
DOI: 10.1017/jfm.2012.132
- Shagapov V.Sh. and Sarapulova V.V.
Reflection and refraction of acoustic waves at the interface between a gas and a disperse systems //
Journal of Applied Mechanicsand Technical Physics. 2015. V. 56, No. 5. Pp. 838–847.
DOI: 10.1134/S0021894415050107
- Shagapov V.Sh. and Sarapulova V.V.
Characteristic features of rarefaction and refl ection of sound at the boundary of a bubble liquid //
Acoustical Physics. 2015. V. 61, No. 1. Pp. 37–44.
DOI: 10.1134/S1063771014060153
- Gimaltdinov I.K. and Galimzyanov M.N.
Dynamics of localized pulse in bubble liquid //
Proceedings of the Mavlyutov Institute of Mechanics. 2014. V. 10. Pp. 38–43 (in Russian).
DOI: 10.21662/uim2014.1.007
- Agisheva U.O. and Galimzyanov M.N.
Evolution of pressure waves acting on a bubble liquid through adjacent boundaries //
Journal of Physics: Conf. Series. 2019. V. 1158. 022008.
DOI: 10.1088/1742-6596/1158/2/022008
- Agisheva U.O. and Galimzyanov M.N.
Low-intensity pressure waves in a stratified bubbly liquid //
Journal of Physics: Conf. Series. 2019. V. 1400. 077045.
DOI: 10.1088/1742-6596/1400/7/077045
- Carey V.P.
Thermodynamic Analysis of the Intrinsic Stability of Superheated Liquid in a Micromechanical Actuator with Elastic Walls //
Microscale Thermophysics Engineering. 2000. V. 4, No. 2. Pp. 109–123.
DOI: 10.1080/108939500404025
- Shagapov V.Sh., Koledin V.V. and Vakhitova N.K.
Stability of an overheated liquid containing vapor-gas bubbles //
Journal of Applied Mechanics and Technical Physics. 2013. V. 54, No. 5. Pp. 742–755.
DOI: 10.1134/S0021894413050076
- Koledin V.V. and Shagapov V.Sh.
On the dynamics of vapor bubble growth in the super heated liquid //
Journal of Applied Mathematics and Mechanics. 2013. V. 77, No. 5. Pp. 754–767 (in Russian).
https://elibrary.ru/item.asp?id=20406061
- Varaksin A.Y.
Fluid dynamics and thermal physics of two-phase flows: problems and achievements //
High Temperature. 2013. V. 51, No. 3. Pp. 377–407.
DOI: 10.1134/S0018151X13030073
- Shagapov V.Sh., Galimzyanov M.N. and Vdovenko I.I.
Acoustics and stability of an overheated liquid with gas bubbles //
Journal of Applied Mechanics and Technical Physics. 2019. V. 60, No. 3. Pp. 473–482.
DOI: 10.1134/S002189441903009X
- Agisheva U.O., Galimzyanov M.N. and Vdovenko I.I.
Acoustic properties of overheated liquid with gas nuclei during temperature increasing //
Journal of Physics: Conf. Series. 2019. V. 1268. 012014.
DOI: 10.1088/1742-6596/1268/1/012014
- Shagapov V.Sh., Galimzyanov M.N. and Vdovenko I.I.
Characteristics of the stability and acoustic properties of superheated liquid with gas nuclei under increasing pressure //
High Temperature. 2019. V. 57, No. 5. Pp. 712–717.
DOI: 10.1134/S0018151X19050146
- Shagapov V.Sh., Galimzyanov M.N., Vdovenko I.I. et al.
Characteristic features of sound propagation in a warm bubble-laden water //
Journal of Engineering Physics and Thermophysics. 2018. V. 91, No. 4. Pp. 854–863.
DOI: 10.1007/s10891-018-1809-9
- Shagapov V.Sh., Galimzyanov M.N. and Vdovenko I.I.
Characteristics of the reection and refraction of acoustic waves at normal incidence on the interface between «pure» and bubbly liquids //
High Temperature. 2019. V. 57, No. 2. Pp. 256–262.
DOI: 10.1134/S0018151X1901022X
- Shagapov V.Sh., Galimzyanov M.N. and Vdovenko I.I.
Characteristics of the reection and refraction of acoustic waves at oblique incidence on the interface between “pure” and bub bly liquids //
High Temperature. 2019. V. 57, No. 3. Pp. 425–429.
DOI: 10.1134/S0018151X19020184
- Agisheva U.O., Vdovenko I.I. and Galimzyanov M.N.
Acoustic waves in a superheated liquid with a gas nuclei //
Journal of Physics: Conf. Series. 2019. V. 1158. 022007.
DOI: 10.1088/1742-6596/1158/2/022007
- Nigmatulin R.I., Shagapov V.Sh. and Vakhitova N.K.
Effect of the compressibility of the carrier phase in wave propagation in a bubble medium //
Doklady. Akad. Nauk SSSR. 1989. V. 304, No. 5. Pp. 1077–1081.
- Nakoryakov V.E. and Shreiber I.R.
[Propagation of small perturbations in a vapor–liquid mixture] Rasprostranenie malih vozmuscheniy v parojidkostnoi smesi //
Problems of Thermophysics and Physical Hydrodynamics. Novosibirsk: Nauka, 1974. Pp. 161–166 (in Russian).
- Landau L.D., Lifshits E.M. Hydrodynamics. Moscow: Fizmatlit. Vol. 6. 2001. 736 p (in Russian).
- Bazarov I.P. Thermodynamics. Moscow: High School, 1991. P. 376 p (in Russian).
- Shagapov V.Sh., Yalaev A.V.
On the theory of the bulk boiling of a liquid with transition into a metastable state //
Theoretical Foundations Of Chemical Engineering. 2012. V. 46. No 4. Pp. 348–358.
DOI: 10.1134/S0040579512010149
- Vargaftik N.B.
[Handbook of Thermophysical Properties of Gases and Liquids] Spravochnik po teplofizicheskim svoistvam gazov i jidkostei.
Moscow: Nauka, 1972. P. 720 (in Russian).
- Shagapov V.Sh.
[On the theory of sound propagation in fog] K teorii o rasprostranenii zvuka v tumane //
Izvestiya AN SSSR Fizika atmosfery i okeana. 1988. V. 24. No. 5. Pp. 506-512 (in Russian).
- Gibbs J.W. Thermodynamics. London: Longmans, Green and Company, 1906.