Article outline

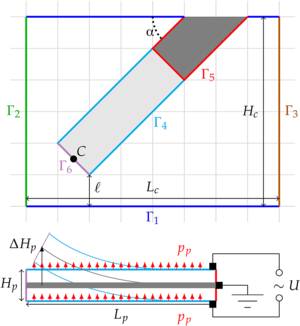
The paper proposes a two-dimensional computer model of the fluid flow in a flat channel under the action of the applied pressure drop. A flat ceramic piezoelectric actuator is immersed in the liquid at an angle α, bending in the transverse direction in proportion to the applied electric voltage. With a piezoelectric drive resting in the channel, a Poiseuille flow is created through the hydraulic resistance formed by the piezoelectric element. With periodic oscillations of the drive, the nature of the fluid flow changes significantly and depends on the frequency of oscillations.

The flow of an incompressible fluid is described by the Navier-Stokes and continuity equations, and the piezo drive deformations were determined using the Lame equation. The following boundary conditions were set for the velocity: no-slip conditions were fulfilled on the surface of the channel and the piezo-actuator, the pressure at the inlet and outlet was different by a predetermined value. The boundary conditions for the deformation were specified in the form of Neumann conditions on the flexible part of the piezoelectric drive (constant pressure) and in the form of Dirichlet conditions on the rigid part (zero displacement). The nonlinear Nav-Stokes equations were solved by the Newton method with the initial approximation for solution by the Picard method. Time discretization was carried out according to the implicit first-order Euler scheme. For numerical simulation, the equations were written in a variational form and solved in a package of numerical simulation of partial differential equations by the finite element method FreeFem ++. The relationship between the fluid velocity field and the strain field of the piezo drive was determined as follows: the no-slip condition of the fluid on the surface of the piezo drive means that the fluid velocity coincides with the strain rate of the piezo drive; the fluid flow creates an uneven pressure field, which acts as a normal component of the stress field on the surface of the piezoelectric drive and reduces the deformation of the piezoelectric drive due to the resistance of the medium.

The simulation was carried out on two two-dimensional matched computational meshes. First, the equations of elasticity were solved on the mesh determining the piezoelectric drive. Based on the obtained deformation field, at each time step, the computational mesh for the channel was rebuilt. Then, the equations of hydrodynamics were solved on the computational mesh of the channel. To prevent the occurrence of an error associated with the movement of nodes of one finite element (FE) inside another FE (the appearance of negative volumes), when remeshing for the channel, an algorithm for “safe” remeshing was developed (in case of negative volumes, the transformation coefficient changes, otherwise transformation is provided; the verification is repeated until the transformation of the computational mesh is complete).

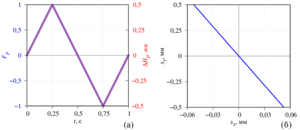
The deformations and equivalent stresses of von Mises on a piezodrive are calculated. Piezo actuator deformations linearly depend on the applied pressure. The equivalent von Mises stresses are distributed nonlinearly along the flexible part of the piezoelectric drive and are concentrated near its rigid part.

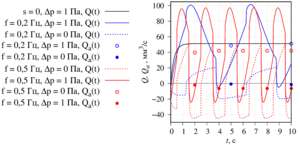
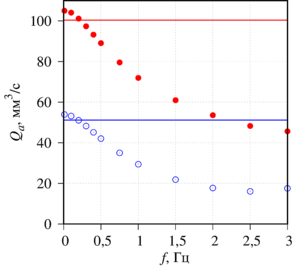
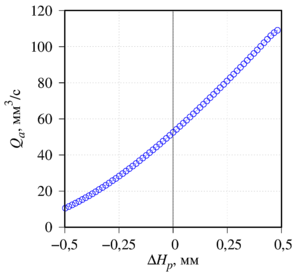
The influence of the geometry of the channel and the hydrodynamic resistance formed by the piezodrive on the dynamics of the fluid flow is analyzed. With a symmetric control signal supplied to the piezoelectric drive, the asymmetry of the geometry leads to a violation of the symmetry of the fluid flow within the period, both in terms of fluid flow rate and in time. In the absence of a pressure drop at low frequencies of the oscillations of the piezoelectric element (of the order of the inverse relaxation time of the velocity), the period-average liquid flow rate is nonzero and increases with increasing frequency. In the presence of a pressure differential between the inlet and outlet of the channel, the average liquid flow rate is proportional to the pressure drop; at low frequencies - inversely proportional to frequency; with increasing frequency - goes to saturation.

Piezo actuator deformations have a significant effect on fluid dynamics. But the fluid also affects the deformation of the piezoelectric drive. The maximum voltage corresponds to the maximum deformation in the air, but when the piezoelectric element is immersed in a liquid, the medium resists deformation. The resistance value is determined by the differential pressure of the liquid relative to opposite sides of the surface of the piezoelectric actuator. With increasing frequency, the medium resistance increases quadratically, and the effect becomes noticeable at frequencies from 20 Hz.

Based on the results of numerical modeling, various variants of new microfluidic technical devices generating a fluid flow using a piezoelectric transverse bending drive are proposed: a micropump creating a closed-circuit flow; fluid flow regulator and fluid volume dispenser.