The dynamics of the behavior of a gas and a gas-drop mixture in a point explosion studied using the analytical solution of L.I. Sedov, constructed on the basis of a self-similar solution for the problem of a point explosion in a gas of spherical configuration. The analysis of the actual problems of theory of point explosion in connection with their use in studying the processes of explosive destruction of cosmic bodies in the atmosphere, where the obtained analytical solutions of Sedov were used as the initial conditions for further numerical implementation of the set problems. The works in which the problems of a point explosion in a dusty medium were considered in a self-similar formulation are noted. A self-similar solution of the Sedov problem of a point explosion in a gas and a gas-drop mixture is presented. A comparative analysis of the obtained solutions in gas and gas-drop mixture in the form of dynamic characteristics of the forming wave flows is made. It is shown that the use of an analytical solution makes it possible to estimate the parameters of shock waves in the studied medium and to obtain estimates of the efficiency of the energy-absorbing properties of a gas-drop mixture in comparison with a gas for conditions of equal initial energy action, which qualitatively does not contradict the existing solutions of other authors and the corresponding experimental data. The possibility of using the obtained analytical solutions in further research for approbation the applied numerical methods in solving problems of the dynamics of gas-liquid flows is noted.
L.I. Sedov’s problem,
self-similar solution,
point explosion,
perfect gas,
gas-drop mixture
Purpose. Comparative analysis of the self-similar solution of the Sedov problem on a point explosion in a gas and a gas-drop mixture.
Methodology. Modeling the dynamics of one-dimensional spherical shock waves in a gas and gas-drop mixture is performed by using analytical self-similar solutions for Sedov’s problem of a point explosion.
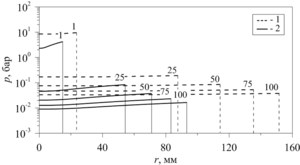
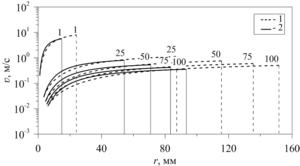
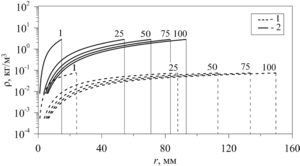
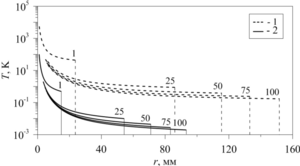
Findings. For the analytical solution of the Sedov problem on a point spherical explosion in gas, the following initial conditions were chosen: the explosion energy
Value. As a result of the conducted studies, it is shown that the use of an analytical solution makes it possible to estimate the parameters of shock waves in a gas-drop mixture and to obtain estimates of the efficiency of its damping properties in comparison with a gas for conditions of equal initial energy action, which qualitatively does not contradict the available experimental data. The obtained analytical solutions can be applied in further research to approbation numerical methods developed to solve a wide range of problems of the dynamics of gas-liquid flows.