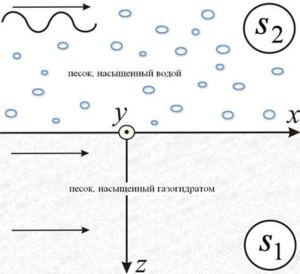
In this paper, we consider the process of the Stoneley wave’s propagation along the interface of two media, where
the upper medium is represented by sand saturated with water, and the lower one by sand saturated with gas hydrate. In a rectangular coordinate system,
the directions of the axes are selected for the case when the plane of the partition is
surface acoustic waves,
stoneley wave,
dispersion equation
Much attention is paid by researchers to surface acoustic waves, since the areas of their application and study for continuum mechanics are multifaceted. These elastic waves propagate along the free surface of a solid body or the boundary with other media and attenuate with distance from the boundary. At present, the theory of acoustic waves makes a significant contribution to the study of a large number of phenomena. A significant number of works are devoted to the physical properties, applications and characteristics of these waves under various environmental conditions, with various complicating factors. It is known that surface waves can be with vertical and horizontal polarization, and Rayleigh, Love and Stoneley waves can be attributed to the most common special cases. Of greatest interest is the problem of the propagation of a surface harmonic wave along the interface between two rigidly glued media, which was first published in the work of the British seismologist Robert Stoneley in 1924. These waves are still being investigated with various complicating circumstances in geophysics, seismology to assess rock permeability, distribution, reservoir thickness, etc. Using these waves, one can estimate rock permeability, hydrate reservoir thickness, and obtain Stoneley wave velocities.
In this paper, we consider the process of the Stoneley wave’s propagation along the interface of two media, where the upper medium is represented by sand saturated with water, and the lower one by sand saturated with gas hydrate. In a rectangular coordinate system, the directions of the axes are selected for the case when the plane of the partition is z=0. We assume that the Stoneley wave has vertical polarization, i.e. there is no horizontal transverse displacement. The harmonic wave propagates to a sufficiently remote distance from the source of the explosion and is represented by the sum of longitudinal and transverse waves in each half-space. For description the mathematical model, wave equations, equations for displacement of particles and components of stress tensors are used, which are supplemented by boundary conditions. As a result of finding analytical solutions in the form of a harmonic traveling wave for displacements, potentials, vectors of longitudinal and transverse waves, a dispersion equation for determining the velocity of the Stoneley wave is obtained. With using this equation and experimental values of the velocities of longitudinal and transverse waves in saturated porous media, it is possible to find the Stoneley wave velocity depending on various parameters of the porous medium.