Article outline

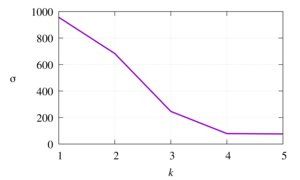
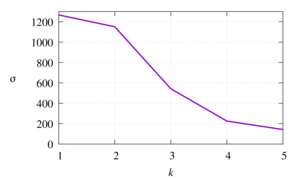
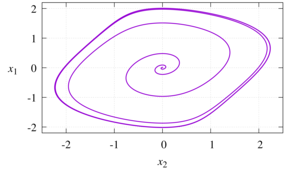
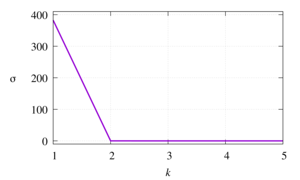
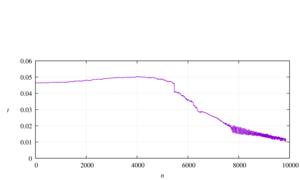
In the general sense, a dynamic system is a mathematical model of the evolution of a real system whose state at any given time is uniquely determined by its initial state. Often, when studying dynamic systems, the main source of information on the behavior of the object under study is a set of values of the observed quantity taken at certain (successive) points in time, the so-called time series. One of the main tasks in analyzing time series is to reconstruct the dynamic system that generated the series. For example, for a locally parameterized surface, Takens reconstructed the behavior of the original dynamic system using Euclidean coordinates (manifold) of integer dimension. To describe the behavior of nonlinear dynamic systems, so-called attractors are widely used. The objectives of this study are to estimate the dimension of the attractor of classical dynamic systems described by the Van der Pol, Henon, and logistic model equations, as well as to identify significant parameters of the percolation sensor system during evaporation of aluminum electrolytes by determining the smoothness of the deterministic model of volt-ampere time series. Identification of systems (reconstruction of equations) from discrete sequences of experimental data (time series) allows us to understand the dynamics of processes changing over time and to predict trends. By identifying significant parameters (attractor dimension) of the time series, we determine which values can be neglected and which values need to be taken into account. The observed significant parameters during the study of aluminum wire evaporation when immersed in a chemical solution were confirmed by the calculations presented in the work. To estimate the attractor dimension of the dynamic system, the principal component method is used, the idea of which is to rotate the coordinate axes in a multidimensional space and select the directions along which the motion mainly develops. The principal component method is a fast way to identify components on a sample of no more than 10 thousand data, while maintaining the accuracy of the solution. This method is a special case of filtered embedding and is useful in the presence of measurement noise. The dimensions of the attractor for the Van der Pol, Henon (at certain fixed coefficients) and logistic model equations are determined, which are equal to two, three and two, respectively. Let us consider the volt-ampere time series obtained from the study of the evaporation of aluminum wire when immersed in a chemical solution. We divide the series of n = 9800 values into 3 parts corresponding to different stages. We study the second stage, responsible for the transition from macro or micro-sized to nanosized forms, since this part is most strongly exposed to various environmental parameters. Using the principal component method, the eigenvalues of the covariance matrix will be equal to 254.607831, 0.032616, 0.008797, 0.004131, 0.002689. It is evident that the attractor dimension is two. The Hurst index of the volt-ampere time series of the percolation sensor during evaporation of aluminum electrolytes is determined, approximately equal to 0.7. Consequently, the values of this time series are strongly correlated (persistent).