The paper presents a generalized mathematical model and numerical investigation of the problem of acoustic scattering from a single sound-permeable sphere during the passage of two types of waves - spherical from a monopole radiation source and a plane one. In solving the Helmholtz equation, a numerical technique based on the fast method of multipoles is used, which allows achieving high accuracy of the results obtained at the lowest cost of computer time. The calculations are compared with known experimental data and a good agreement is obtained. The formulas for calculating the main characteristic of the scattering field (the total scattering cross section) for a sound-permeable sphere are generalized. The effect on this characteristic of the physical parameters of media outside and inside the sphere, such as the density and speed of sound, is shown. A numerical parametric analysis of the pressure distribution around a single sound-permeable sphere for different values of the wave radius, density, and speed of sound of the outer and inner medium of the sphere is carried out. The obtained results will later be used for test verification calculations for the numerical solution of the generalized problem of acoustic scattering of a set of sound-permeable spheres (coaxial or arbitrarily located in space).
acoustic scattering,
a monopole radiation source,
a plane wave,
a sound-permeable sphere,
a total scattering cross section
Purpose: a generalization of the numerical model to determine the field inside and around a single sound-permeable sphere by passing the two types of waves: a spherical wave from a monopole source and a plane wave.
Methodology: in solving the Helmholtz equation using a numerical technique based on the fast multipole method.
The findings of research:
1. the technique of the multipole expansion for permeable sphere is generalized. The expansion formulas are obtained for two particular cases of the external field (a monopole radiation source and a plane wave);
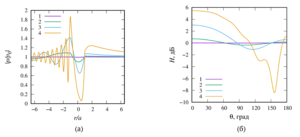
2. a comparison of the calculation results of this work with known experimental data have been made and gave good agreement;
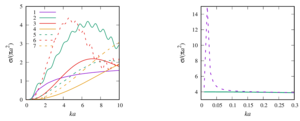
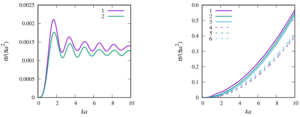
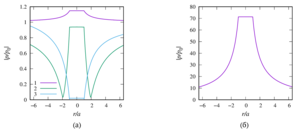
3. the formulas for the total scattering cross section for a sound-permeable sphere are generalized. A numerical analysis of the influence of such physical parameters of the external and internal media on this characteristic as the speed of sound and density with a change in the value of the wave radius was made;
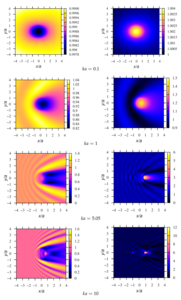
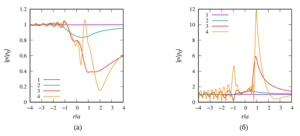
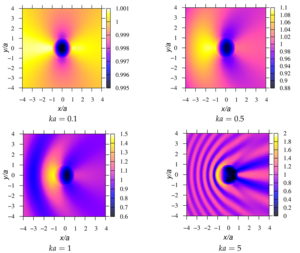
4. a numerical parametric analysis of the pressure distribution around a single sound-permeable sphere for different values of the wave radius, density, and velocity of sound of media inside and outside the sphere is carried out. It is shown that for certain values of the parameters, a ”shadow“ zone may appear behind the sphere (Poisson spot) or, conversely, ”illumination“ of the zone, when the drop is a spherical liquid lens.
Value: The obtained results will subsequently be generalized to perform test calculations for the generalized problem of acoustic scattering of a set of sound-permeable spheres (both coaxial and arbitrarily located in space).