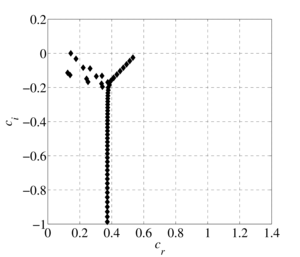
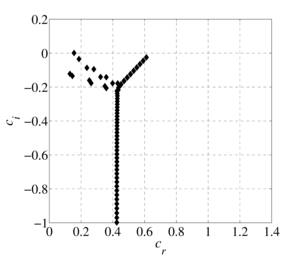
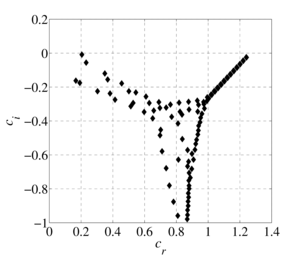
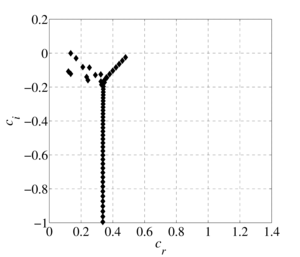
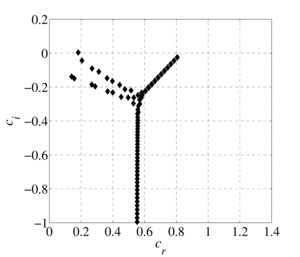
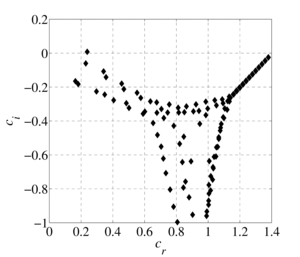
The flow of a viscous model fluid in a flat channel with a non-uniform temperature field is considered. The problem of the stability of a thermoviscous fluid is solved on the basis of the derived generalized Orr-Sommerfeld equation by the spectral decomposition method in Chebyshev polynomials. The effect of taking into account the linear and exponential dependences of the fluid viscosity on temperature on the spectral characteristics of the hydrodynamic stability equation for an incompressible fluid in a flat channel with given different wall temperatures is investigated. Analytically obtained profiles of the flow rate of a thermovisible fluid. The spectral pictures of the eigenvalues of the generalized Orr-Sommerfeld equation are constructed. It is shown that the structure of the spectra largely depends on the properties of the liquid, which are determined by the viscosity functional dependence index. It has been established that for small values of the thermoviscosity parameter the spectrum compares the spectrum for isothermal fluid flow, however, as it increases, the number of eigenvalues and their density increase, that is, there are more points at which the problem has a nontrivial solution. The stability of the flow of a thermoviscous fluid depends on the presence of an eigenvalue with a positive imaginary part among the entire set of eigenvalues found with fixed Reynolds number and wavenumber parameters. It is shown that with a fixed Reynolds number and a wave number with an increase in the thermoviscosity parameter, the flow becomes unstable. The spectral characteristics determine the structure of the eigenfunctions and the critical parameters of the flow of a thermally viscous fluid. The eigenfunctions constructed in the subsequent works show the behavior of transverse-velocity perturbations, their possible growth or decay over time.
thermoviscous liquid,
spectra of eigenvalues,
hydrodynamics instability
The purpose of this work is to research the hydrodynamic stability of thermoviscous liquids flow with monotonic temperature dependences of viscosity and the search for parameters characterizing the flow regimes.
Solution methods. The problem of thermoviscous fluid stability is solved on the basis of the generalized Orr-Sommerfeld equation obtained earlier by the spectral decomposition method in Chebyshev polynomials.
The study found:
At present, a sufficient reserve has been accumulated in the study of the stability of flows of liquids in flat channels, however, in studying this problem, the effect of the temperature factor on the change of flow regime is often neglected. Viscous fluid flows occur in a number of industries in the operation of various technical installations and devices, and in the implementation of a number of technological processes. In such cases, the problem of identifying the characteristics of such a flow under various conditions is important. From the point of view of energy efficiency, the laminar regime is important, on the other hand, when considering the efficiency of heat and mass transfer, it is turbulent. Fluid viscosity is an important parameter that determines the flow patterns.
The flow of a viscous model fluid in a plane-parallel channel with a non-uniform temperature field is considered. The influence of taking into account the linear and exponential dependences of the fluid viscosity on temperature on the spectral characteristics of the hydrodynamic stability equation for an incompressible fluid in a flat channel at different wall temperatures is investigated. Analytically obtained profiles of the flow rate of a thermoviscous fluid. At small values of the viscosity change parameter, the velocity profile is similar to the Poiseuille profile, and as it increases, the maximum value of the velocity profile tends towards the heated channel wall. This phenomenon is explained by the fact that the viscosity of the fluid near the hot wall is less than that of the fluid near the cold wall, and therefore the velocity in the region of the heated wall will be greater. The problem of the stability of a thermal viscous fluid is solved on the basis of the generalized Orr-Sommerfeld equation obtained earlier by the spectral decomposition method in Chebyshev polynomials. The spectral pictures of the eigenvalues of the generalized Orr-Sommerfeld equation are constructed. It is shown that the structure of the spectra largely depends on the properties of the liquid, which are determined by the viscosity functional dependence index. It was established that at small values of the thermal viscosity parameter, the spectrum is comparable to the spectrum for isothermal fluid flow, however, as it increases, the number of eigenvalues and their density increase, that is, there are more points at which the problem has a nontrivial solution. The stability of the flow of a thermally viscous fluid depends on the presence of an eigenvalue with a positive imaginary part among the entire set of eigenvalues found with fixed Reynolds number and wavenumber parameters. It is shown that for fixed values of the Reynolds number and wave number with increasing thermal viscosity parameter, the flow can become unstable. The spectral characteristics determine the structure of the eigenfunctions and the critical parameters of the flow of a thermally viscous fluid. In this case, the eigenfunctions demonstrate the behavior of transverse-velocity perturbations, their possible growth or decay over time.
Findings. It has been established that taking into account the dependence of viscosity on temperature rather strongly influences conclusions regarding hydrodynamic stability, which is certainly important when analyzing flow regimes in heat exchangers. With the same values of Reynolds numbers and wave numbers describing stable flow regimes, an increase in the thermal viscosity parameter can lead to unstable modes. It should be noted that in this case a qualitative change occurs in the structure of the spectra of eigenvalues. The spectral characteristics of the flow are an important part in analyzing the flow regimes of liquids.