Многофазные системы

Nasibullaeva E.Sh. Numerical simulation of acoustic scattering from coaxial sound-penetrable spheres. Multiphase Systems. 14 (2019) 2. 115–124 (in Russian).

2019. Vol. 14. Issue 2, Pp. 115–124
URL: http://mfs.uimech.org/mfs2019.2.016
DOI: 10.21662/mfs2019.2.016

Numerical simulation of acoustic scattering from coaxial sound-penetrable spheres

Nasibullaeva E.Sh.

Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia

Abstract

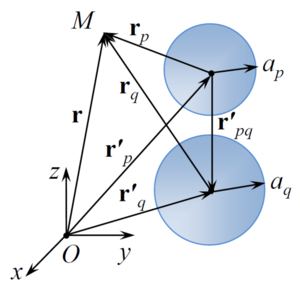
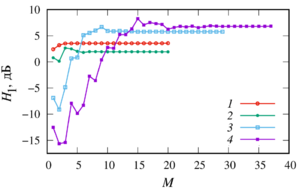
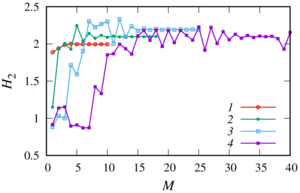
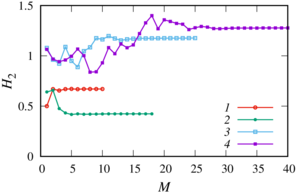
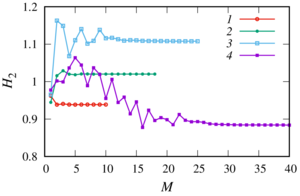
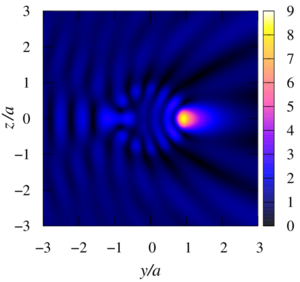
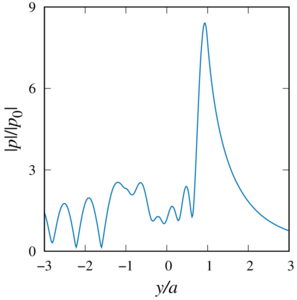
This paper presents a generalisation of the mathematical model and numerical study of the acoustic scattering problem from multiple spheres in the case of spheres through which the wave passes and whose centers are located on the same axis (the case of sound-penetrable and coaxial spheres) under the action of spherical waves from a monopoly radiation source arbitrarily located in space. When solving the Helmholtz equations, a numerical technique based on the fast multipole method has been adapted for this task, which allows one to achieve high accuracy of the results obtained with minimal computer time. Comparison of the different approaches to truncation infinite series in the expansion showed the following: the result with a good degree of accuracy by a single calculation gives approach based on the truncation of all the rows with a fixed number in each expansion, and the result with a certain degree of accuracy gives an approach based on comparing two consecutive values of the sum of the series. A numerical parametric analysis of the pressure distribution inside and outside the spheres is carried out for various values of their radii, physical characteristics of the external and internal media, the number of spheres, the distances between the centers of the spheres, the frequency of exposure and the location of the monopole radiation source. It is shown that at certain values of the parameters, the appearance of zones of decrease or increase in pressure behind sound-penetrable spheres is possible. The obtained results will further allow to carry out test calculations to verify the general numerical algorithm for the case of a multitude of spheres arbitrarily located in space.

Keywords

acoustic scattering,
sound-penetrable sphere,
monopole radiation source,
truncation number

The work was partially supported by the state budget funds for the state assignment (No. 0246-2019-0052), RFBR according to the research project No. 17-41-020582-p_a and the Academy of Sciences of the Republic of Bashkortostan according to contract No. 40/9.

Article outline

When an acoustic wave interacts with small obstacles that differ in density and/or compressibility from the main medium, additional (scattered) waves appear that propagate in all directions from the obstacles. This phenomenon is called scattering (diffraction) of sound. Its study is one of the important problems of acoustics, because it is based on many of the practical application of acoustic waves, such as sonar, non-destructive testing equipment, medical scanners, sensing of the atmosphere and ocean, etc. Therefore, the problem of acoustic scattering from small obstacles under external influences is relevant.

In the paper a generalization of mathematical models is presented and numerical studies were made for the problem acoustic scattering from multiple spheres in the case of a spheres through which the wave passes and whose centers are located on the same axis (the case of sound- penetrable and coaxial spheres) under the influence of a spherical wave from the monopoly of the radiation source arbitrarily located in space.

Purpose: investigation of scattering of an acoustic wave from sound- penetrable spheres (spheres through which surface a wave can pass) with centers located on the same axis in the presence of a monopole radiation source.

Methods: When solving the Helmholtz equations, a numerical technique based on the fast multipole method was adapted for the problem under consideration. This calculation technique allows to achieve high accuracy of the results with minimal use of computer time. The problem is considered in axisymmetric formulation. As a result of numerical modeling, program codes were written in the Fortran 90 language.

The following numerical studies were made:

testing of the algorithm carried out for the cases that are presented in a similar theoretical and experimental (for a single sphere) works. Testing showed the correctness of the data obtained according to the presented methodology;
different approaches to the truncation of the infinite series in the expansion;
the pressure distribution inside and outside the spheres for various physical parameters, both external and internal for the sphere of media, the number of spheres and the distance between their centers, as well as for different values of the frequencies and the location (relative to the axis connecting the centers of the spheres) of the monopole radiation source.

As a findings of the research, it has been determined that

the result with a good degree of accuracy using one calculation gives an approach based on the truncation of all series with a fixed number in each expansion. To obtain a result with a certain degree of accuracy, it is necessary to use an approach based on a comparison of two consecutive values of the sum of a series;
at certain parameter values, zones of decreasing or increasing pressure behind the sound-penetrable spheres may appear.

Value: The generalized model and calculation procedure in the future will allow to made parametric analysis in a wider range of parameters, including the different values of the radii of the spheres, the distance between their centers, the location and frequency of the monopole radiation source, physical parameters of the surrounding and internal environments, etc. Besides the results obtained will allow to carry out test calculations to verify the general numerical algorithm for the case of many spheres arbitrarily located in space.

References

Nasibullaeva E.Sh. [Investigation of scattering from soundproof single sphere under external influence]. Trudy Instituta mekhaniki im. R.R. Mavlyutova Ufimskogo nauchnogo tsentra RAN Multiphase systems [Proceedings of the Institute of Mechanics. R.R. Mavlyutov Ufa Scientific Center, Russian Academy of Sciences]. 2017. V. 12, No. 1. Pp. 73–82 (in Russian).
DOI: 10.21662/uim2017.1.011
Gumerov N.A., Duraiswami R. Computation of scattering from N spheres using multipole reexpansion // J. Acoust. Soc. Am. 2002. Vol. 112, No. 6. P. 2688–2701.
DOI: 10.1121/1.1517253
Skaropoulos N.C., Yagridou H.D., Chrissoulidis D.P. Interactive resonant scattering by a cluster of air bubbles in water // J. Acoust. Soc. Am. 2003. Vol. 113, No. 6. Pp. 3001–3011.
DOI: 10.1121/1.1572141
Grinchenko V.T., Vovk I.V., Macypura V.T. [Osnovy akustiki] Basics of acoustics. K: Naukova Dumka, 2009. P. 867 (in Russian).
Korn G.A., Korn Th.M. Mathematical Handbook for Scientists and Engineers. McGraw Hill Book Company, 1968. 943 p.
Nasibullaeva E.Sh. [Investigation of acoustic scattering from a pair soundproof spheres under external influence]. Mnogofaznye sistemy [Multiphase Systems]. 2019. V. 14, No. 1. Pp. 44–51 (in Russian).
DOI: 10.21662/mfs2019.1.006
Duda R.O., Martens W.L. Range dependence of the response of a spherical head model // J. Acoust. Soc. Am. 1998. Vol. 104. Pp. 3048–3058.
DOI: 10.1109/ASPAA.1997.625597
Antoine X., Chniti C., Ramdani K. On the numerical approximation of high-frequency acoustic multiple scattering problems by circular cylinders // J. Comput. Phys. 2008. Vol. 227, No. 3. Pp. 1754–1771.
DOI: 10.1016/j.jcp.2007.09.030
Chew W.C., Jin J.M., Michielssen E., Song J. Fast and Efficient Algorithms in Computational Electromagnetics. Artech HouseAntennas and Propagation Library, Norwood, 2001. 932 p.
Zhang S., Jin J. Computation of special functions. NY: Wiley-Iterscience, 1996. 717 p.
Nasibullaeva E.Sh. [The study of acoustic scattering from a single sound-permeable sphere]. Mnogofaznye sistemy [Multiphase Systems]. 2018. V. 13, No. 4. Pp. 79–91 (in Russian).
DOI: 10.21662/mfs2018.4.012
Kapodistrias G., Dahl P.H. Effects of interaction between two bubble scatterers // J. Acoust. Soc. Am. 2000. Vol. 107. Pp. 3006–3017.
DOI: 10.1121/1.429330