Tukmakov D.A.
Numerical study of velocity slip of phases during the passage of a shock wave of low intensity from a pure gas
to a dusty medium. Multiphase Systems. 14 (2019) 2. 125–131 (in Russian).
Numerical study of velocity slip of phases during the passage of a shock wave of low intensity from a pure gas to a dusty medium
Tukmakov D.A.
Institute of Mechanics and Engineering, Kazan Scientific Center of the RAS, Kazan
Abstract
In this paper, the process of the movement of a direct shock wave from a pure gas into a dusty medium is numerically
modeled. The mathematical model took into account the viscosity, compressibility and thermal conductivity of the
carrier phase. Also, the modeling technique made it possible to describe the interphase force interaction, which
included the Stokes force, the dynamic force of Archimedes, the strength of the attached masses. In addition,
interfacial interaction included heat transfer between the carrier and dispersed phases. The numerical solution was
carried out using the explicit finite-difference method, with the subsequent application of the nonlinear correction
scheme for the grid function. As a result of numerical calculations, it was revealed that with an increase in the linear
particle size of the gas suspension, the velocity slip between the carrier and dispersed phases increases. Numerical
modeling also showed that the absolute value of the difference between the velocities of the carrier and the dispersed
phase reaches the largest value at the leading edge of the compression wave. The revealed regularities can be
explained by the fact that the particles of the dispersed phase are assumed to be spherical in shape. Due to this, a
multiple increase in particle size leads to a three-fold increase in their mass, a twofold increase in the area of one
particle and a three-fold decrease in the number of particles. Thus, an increase in particle size leads to a decrease
in the area of interfacial contact and an increase in the inertia of the particles, which in turn affects the interfacial
velocity slip.
Keywordsnumerical simulation,
Navier-Stokes equation,
dusty media,
shock waves
This work was supported by the Russian Foundation for Basic Research Grant No 19-01-00442.
Article outline
Purpose. The processes associated with the movement of multiphase media are found both in nature and
in industrial technologies. Therefore, one of the relevant sections of fluid and gas mechanics is the study of the dynamics of inhomogeneous media,
including gas suspensions of droplets and solid particles. Since in many cases the experimental study of such flows is difficult, mathematical modeling
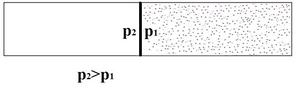
is essential. The article simulated the movement of a direct shock wave from a pure gas into a dusty medium.
Methodology. In this work, the dynamics of gas suspension of solid particles - a dusty medium is described on the basis of a two-speed,
two-temperature model taking into account the inter-component heat transfer, as well as the inter-component force interaction, which includes
the Stokes force, the dynamic force of Archimedes and the strength of the attached masses.
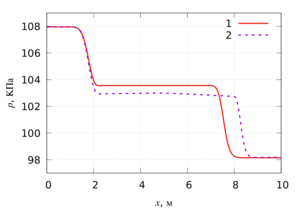
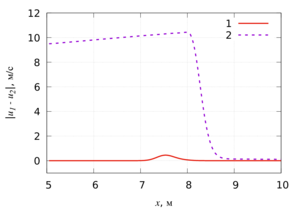
Findings. Numerical simulation shows that during the movement of a shock wave through a dusty medium, a decrease in the dispersion
of particles of a gas suspension located in a low-pressure chamber leads to an increase in pressure in the compression wave and to a decrease
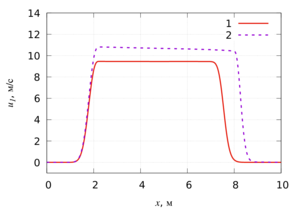
in the velocity of propagation of the shock wave. From the calculations it follows that in a gas suspension with a larger particle size,
a higher velocity of the gas flow is observed. At the same time, in a dusty medium, an increase in the linear particle size leads to a decrease
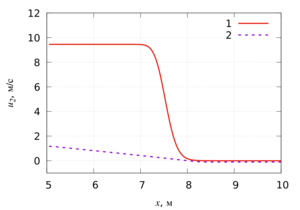
in the velocity of the dispersed phase. For finely dispersed gas suspensions, high-speed sliding is insignificant. In this case, for gas suspensions
with both a coarse and finely dispersed solid phase, the largest value of the absolute value of the velocity difference between the carrier and disperse
phase is observed at the leading edge of the compression wave. In a coarse-grained gas suspension, an increase in the absolute value of the velocity
difference between the solid and gaseous phases is observed from the contact area between the dusty medium and pure gas to the leading edge
of the compression wave.
Originality. In the process of the movement of a direct shock wave from pure gas into a dusty medium with an increase in particle size,
an increase in the velocity of the disturbance and a decrease in pressure at the leading edge of the compression wave occur. The largest value
of the modulus of the velocity difference between the carrier and the dispersed phase is observed at the leading edge of the compression wave
in front of the unperturbed medium.
References
- Nigmatulin R.I. [The dynamics of multiphase media] Dinamika mnogofaznyh sred. Part 1. M.: Science. 1987. 446 p. (in Russian)
- Kutushev A.G. [Mathematical modeling of wave processes in aerodispersed and powdery media].
Matematicheskoe modelirovanie volnovyh processov v aerodispersnyh i poroshkoobraznyh sredah. SPb.: Subsoil. 2003. 284 p. (in Russian)
- Fedorov A.V., Fomin V.M., Khmel T.A. [Wave processes in gas-suspended particles of metals] Volnovye processy v
gazovzvesyah chastic metallov. 2015. Novosibirsk. 301 p. (in Russian)
- Verevkin A.A., Tsirkunov Yu.M. [Dispersed impurity flow in a Laval nozzle and working section of a two-phase hypersonic shock tube].
Prikladnaya mekhanika i tekhnicheskaya fizika. [Applied Mechanics and Technical Physics]. 2008. No. 5. Pp. 102–113. (in Russian)
- Pakhomov M.A., Terekhov V.I. [The effect of droplet evaporation on the flow structure and heat and mass transfer in a limited swirling
gas-droplet flow due to its sudden expansion] Teplofizika i aeromekhanika. [Thermophysics and Aeromechanics]. 2018. No. 6. Pp. 865–875. (in Russian)
https://elibrary.ru/item.asp?id=36825464
- Sadin D.V. [TVD scheme for tough problems of wave dynamics of heterogeneous media of non-hyperbolic non-conservative type]
Zhurnal vychislitel’noj matematiki i matematicheskoj fiziki. [Journal of Computational Mathematics and Mathematical Physics].
2016. V. 56, No. 12. Pp. 2098–2109. (in Russian)
DOI: 10.7868/S0044466916120152
- Gubaidullin A.A., Dudko D.N., Urmancheev S.F. [Computer-aided modeling of the effects of air shock waves on porous-layer barriers]
Vychislitel’nye tekhnologii. [Computational technologies]. 2001. V. 6, No. 3. Pp. 7–20. (in Russian)
https://elibrary.ru/item.asp?id=13026371
- Balapanov D.M., Urmancheev S.F. [The role of interfacial interactions in the course of gas detonation in an inert porous medium] //
PZhTF [Letters to the journal of technical physics]. 2010. V. 36, No. 13. Pp. 71–80. (in Russian)
https://elibrary.ru/item.asp?id=20327258
- Bolotnova R.Kh., Gainullina E.F. [The study of the damping properties of water foam under the influence of a spherical shock wave]
Izvestiya vysshih uchebnyh zavedenij. Povolzhskij region. Fiziko-matematicheskie nauki. [News of higher educational institutions.
Volga region. Physics and mathematics]. 2017. No. 2(42). Pp. 108—121. (in Russian)
DOI: 10.21685/2072-3040-2017-2-9
- Belyaev P.E., Klinacheva N.L. [The effect of the screening layer of a gas suspension on the force of a shock wave on a rigid wall]
Vestnik YURGU ser. Matematika. Mekhanika. Fizika. [Messenger of South Ural State University Maths. Mechanics. Physics]
2016. V. 8, No. 4. Pp. 49–55. (in Russian)
DOI: 10.14529/mmph160406
- Utkin P.S. [Some computational aspects of the interaction of a shock wave with a cloud of particles in a two-fluid model]
Gorenie i vzryv. [Combustion and Explosion] 2017. V. 10, No. 3. Pp. 53-57. (in Russian)
https://elibrary.ru/item.asp?id=30682321
- You Z., Li B., Wang H., Xie L. Water aerosol formation: Transient process induced by shock waves //
Journal of Aerosol Science. 2017. V. 106. Pp. 100–110.
DOI: 10.1016/j.jaerosci.2017.01.010
- Tada Y., Yoshioka S., Takimoto A., Hayashi Y. Heat transfer enhancement in a gas–solid suspension flow by applying electric field //
International Journal of Heat and Mass Transfer. 2016. V. 93. Pp. 778–787.
DOI: 10.1016/j.ijheatmasstransfer.2015.09.063
- Fletcher C.A. Computation Techniques for Fluid Dynamics. Springer-Verlang. Berlin. 1988. 502 p.
- Muzafarov I.F., Utyuzhnikov S.V. [Application of compact difference schemes to the study of unsteady flows of a compressible gas]
Matematicheskoe modelirovanie. [Mathematical modeling] 1993. No. 3. Pp. 74–83. (in Russian)
http://mi.mathnet.ru/mm1962
- Tukmakov A.L. [Numerical simulation of acoustic flows in resonant gas oscillations in a closed pipe]
Aviacionnaya tekhnika. [Aviation Engineering]. 2006. No. 4. Pp. 33–36. (in Russian)
https://elibrary.ru/item.asp?id=12510457
- Tukmakov D.A. [Numerical modeling of shock-wave flows in a gas suspension with an inhomogeneous concentration of the dispersed phase]
Aviacionnaya tekhnika. [Aviation Engineering]. 2019. No. 1. Pp. 54–59. (in Russian)
https://elibrary.ru/item.asp?id=38027390
- Tukmakov D.A. Numerical study of polydisperse aerosol dynamics with the drops destruction //
Lobachevskii Journal of Mathematics. 2019. V. 40, No. 6. Pp. 824–827.
DOI: 10.1134/S1995080219060234
- Tukmakov D. A. [Numerical modeling of oscillations of an electrically charged heterogeneous medium due to intercomponent interaction]
Izvestiya vuzov. Prikladnaya nelinejnaya dinamika. [News of Universities. Applied nonlinear dynamics]. 2019. V. 27, No. 3. Pp. 73–85. (in Russian)
DOI: 10.18500/0869-6632-2019-27-3-73-85