Article outline

The bending vibrations of a pipeline sagging above an obstacle (ravine) under the action of a tensile force are considered. On both sides of the sagging section of the pipe lies on the elastic supports. The reaction of supports to pipe bending is modeled by a system of springs with certain stiffnesses. The fluid transported through the pipeline is under pressure. The task is to identify the speed and density of the transported fluid by the known frequency spectrum of the bending vibrations of the pipeline system.

The direct problem of determining the natural frequencies from given input parameters (pressure, velocity of the transported fluid, spring elasticity coefficients) was solved earlier. It was shown that with an increase in the velocity parameter, the natural frequencies of the bending vibrations of the pipeline decrease. Moreover, the frequencies fall faster if the fluid density parameter is higher. With an increase in the mass of liquid per unit length of the pipeline, the natural frequencies of the bending vibrations of the pipe decreased. It was observed that with increasing mass flow rate of the liquid through the pipe, the natural frequencies of bending vibrations also decrease. This article solves the inverse problem of identifying the velocity and density of the transported fluid by the known frequencies of bending vibrations. The equation of bending vibrations of the pipeline is described by the Kirchhoff model. The characteristic equation is solved using Ferrari formulas. The general decision is determined. Satisfying the general solution to the boundary conditions, we obtain a homogeneous system of equations. This system gives a frequency equation, which is already solved numerically on a specially developed program in the mathematical package Maple. The method of successive approximations is applied. The calculation results of the program are displayed on a separate file in the form of a table. The program for calculating natural frequencies gives good results. The analysis shows that after the third iteration, the accuracy of the calculation of the velocity and density parameters of the transported liquid is about 10^-3.

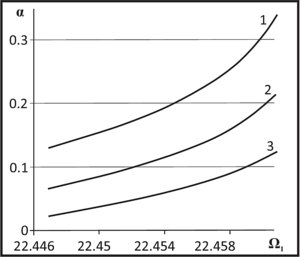
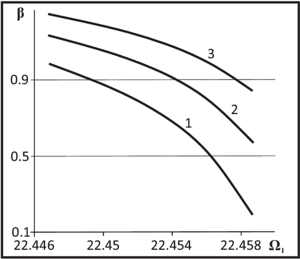
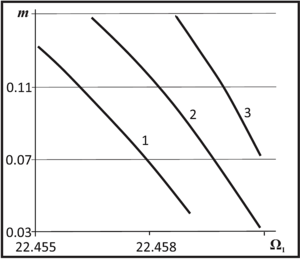
The paper presents the dependences of the velocity and density parameters of the transported liquid on the first natural frequency of the bending vibrations of the pipeline for different fixed values of the second natural frequency. It was found that with an increase in the oscillation frequency, the fluid density parameter inside the pipe decreases. It is determined that with an increase in the natural frequencies of the bending vibrations of the pipeline, the velocity parameter of the transported fluid also increases. It is shown that the two lower frequencies of the bending vibrations of the pipeline can be used to determine the parameters of the velocity and density of the liquid. The dependence of the mass flow rate of the liquid on the first natural frequency of the pipe oscillations is given. It is shown that with an increase in the first eigenfrequency, the mass flow rate decreases.

The results of the study will contribute to the development of methods of acoustic diagnostics and non-destructive testing methods and can find technical application for monitoring and diagnostics of pipeline systems.