Bashirova K.I., Mikhaylenko C.I.
Shock wave reflection from a layer of a finely dispersed medium with low concentrations. Multiphase Systems. 14 (2019) 4. 279–283 (in Russian).
Shock wave reflection from a layer of a finely dispersed
medium with low concentrations
Bashirova K.I.∗, Mikhaylenko C.I.∗∗
∗Ufa State Aviation Technical University, Ufa, Russia
∗∗Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
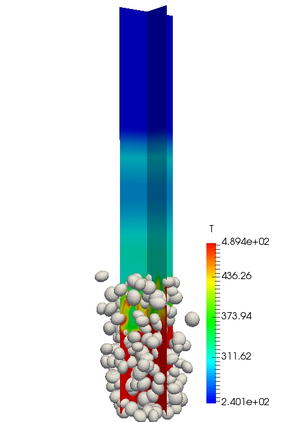
The paper investigates the propagation of a shock wave when interacting with a loosely packed granular medium. The
continuous two-phase mathematical model presented in this work allows one to numerically describe the propagation
of a shock wave in the channel of a shock tube, the achievement of a layer of granular filling by the shock wave, and
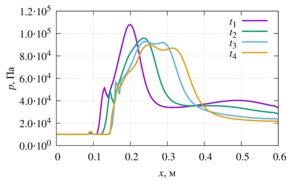
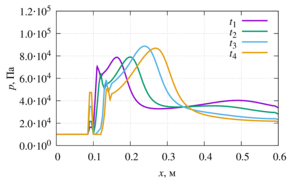
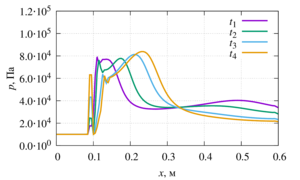
the reflection of the wave. It was shown that the granular medium partially transmits the shock wave, but mostly
corresponds to it. This reflection differs from the reflection of a shock wave from a solid wall. The nature of the
reflection of the shock wave depends on the density of the granules. In particular, it has been shown that a granular
medium of lower density, due to the increased mobility of individual particles, leads to some amplification of the
reflected wave. It is also shown that the reflected wave in this case forms two pronounced peaks. It should be noted
that the pressure passed in the layer of the granular medium, on the contrary, turns out to be the greater, the heavier
the particles of the granular medium.
Keywordsmultiphase systems,
granular media,
shock waves,
mathematical modeling,
OpenFOAM
References
- Kedrinskii V.K. Shock waves in a liquid containing gas bubbles // Combustion, Explosion, and Shock Waves. 1980. V. 16. No 5. Pp. 495-504.
https://elibrary.ru/item.asp?id=35463272
- Parkin B.R., Gilmore F.R., Brode G.A. Shock waves in bubble water. Memorandum RM-2795-PR. Abridged. 1961.
- Gubajdullin A.A., Kutrunov A.V., Rustyumova O.Sh., Yakovleva T.N. [Some questions of the wave dynamics of a liquid with gas bubbles]
Nekotorye voprosy volnovoj dinamiki zhidkosti s puzyr’kami gaza // Itogi issledovanij. Tyumen. 1994. Pp. 23–31.
- Britan A., Ben-Dor G., Shapiro H., Liverts M., Shreiber I. Drainage effects on shock wave propagating through aqueous foams //
Colloids and Surfaces A: Physicochem. Eng. Aspects. 2007. V. 309. Pp. 137–150.
DOI: 10.1016/j.colsurfa.2007.01.018
- Nigmatulin R.I. Dynamics of Multiphase Media. Vol 1 & 2. Hemisphere Publ. Corp New York, United States. 1990. 507 p.
- Fedorov, A.V., Fedorchenko, I.A., Vasilishin, M.S., Karpov, A.G., Ivanov, O.S. Calculation of expansion of a packed bed of a disperse material subjected to pulsed fluidization //
Journal of Applied Mechanics and Technical Physics. 2012. Vol. 53, No. 3. P. 397-407.
DOI: 10.1134/S0021894412030121
- Mikaylenko C.I., Kuleshov V.S. Numerical modelling of inhomogeneity scale of a flow rate behind the porous barrier // Computational Technologies. 2015. V. 20, No 6. Pp. 46–58 (in Russian).
https://elibrary.ru/item.asp?id=25408686
- Mikhailenko С.I., Valeeva Yu.R. Highly dispersed medium sedimentation from air under pressure forces // Numerical methods and programming. 2013. V. 14, No 1. Pp. 328–333 (in Russian).
https://elibrary.ru/item.asp?id=21014483
- Bashirova K.I., Mikhaylenko C.I. Three-dimensional simulation of a shock tube with OpenFOAM software //
Vestnik Bashkirskogo universiteta (Bulletin of Bashkir University). 2018. V. 23, No 3. Pp. 621–626 (in Russian).
https://elibrary.ru/item.asp?id=36476517