Nasibullayev I.Sh.
Reducing the systematic error of the average fluid flow rate in axisymmetric computer model of piezoelectric
micropump. Multiphase Systems. 16 (2021) 1. 20–31 (in Russian).
Reducing the systematic error of the average fluid flow rate in axisymmetric computer model of piezoelectric micropump
Nasibullayev I.Sh.
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
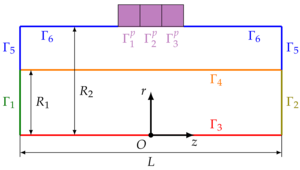
Mathematical and computer models of an axisymmetric coupled problem of interaction of a fluid and an elastic body for the solving partial
differential equations by the finite element method FreeFem ++ software are proposed. In these models, periodic vibrations of annular piezoelectric actuators placed on an elastic
tube of circular cross-section lead to radial deformations of the tube. With a synchronous oscillation of the system of piezoelectric actuators, the average fluid flow rate is zero.
An asymmetric oscillation pattern (micropump mode) results in a nonzero average flow rate. Two types of boundary conditions are considered in the region of contact between the
piezoelectric drive and the tube — Dirichlet and Neumann. The computer model was tested for unsteady fluid flow induced by a pressure gradient applied along the pipe with a circular
cross section. With synchronous oscillation of piezoelectric actuators, a nonzero average fluid flow is a systematic error. This value was compared with the asymmetric oscillation
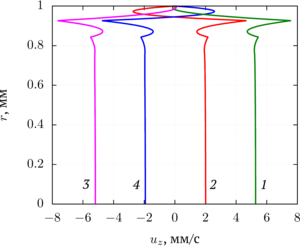
pattern of piezoelectric actuators to determine the contribution of the systematic error to the pump-generated fluid flow rate. Based on the fluid flow velocity profile and the
results of profiling the program code, the optimal parameters of the computational meshes for the channel (dense uniform) and tube walls (nonuniform, consistent with the velocity
profile and reconstructing at each time step) were determined, which reduce the magnitude of the systematic error. The main way to reduce the error is to increase the density of
the computational mesh, which leads to an increase in the required computing resources. An alternative method is proposed for reducing the systematic error due to an additional
pressure drop applied to the channel. Depending on the type of boundary conditions and the number of piezoelectric actuators, this method can reduce the systematic error by 1 − 2
orders of magnitude without increasing the simulation time.
Keywordshydrodynamics,
hydraulic resistance,
piezoelectric actuator,
linear elasticity,
microchannel,
finite element method,
micropump
Article outline
Mathematical and computer models of an axisymmetric coupled problem of interaction of a fluid and an elastic body for solving partial differential
equations by the finite element method FreeFem++ software are proposed. In these models, periodic vibrations of annular piezoelectric actuators placed on an elastic tube of circular
cross-section lead to radial deformations of the tube. With a synchronous oscillation of the system of piezoelectric actuators, the average fluid flow rate is zero. An asymmetric
oscillation pattern (micropump mode) results in a non-zero average flow rate. The equations were written in variational form. Time discretization was carried out by the implicit
Euler method. For nonlinear terms in the Navier-Stokes equation, the Picard scheme was used. To increase the stability of the numerical scheme, artificial compressibility was added
to the continuity equation. Two types of boundary conditions were considered in the area of contact between the piezoelectric drive and the tube - Dirichlet (”hard“ piezoelectric element)
and Neumann (”soft“ piezoelectric element). The equations were solved in the FreeFem++ package by the finite element method. To prevent the appearance of an error associated with the
displacement of the nodes of one finite element inside another finite element (the appearance of negative volumes), when remeshing the computational mesh for the channel, the algorithm
of the ”safe“ remeshing of the computational mesh, developed earlier by the author, was used.
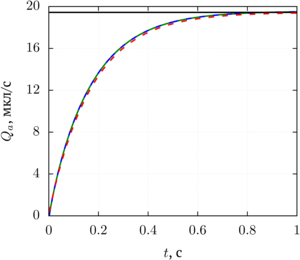
A specific feature of the problem under consideration is that the deformations of the microchannel are small (0.5% of the radius) and at high oscillation frequencies the fluid flow velocity is high (several mm/s). The computer model was tested for an unsteady fluid flow induced by a pressure gradient applied along the layer in a pipe with a circular cross section (Poiseuille flow). The errors of numerical simulation for the instantaneous value of the fluid flow rate and the characteristic relaxation time of the velocity (the time for establishing a constant flow) did not exceed 1 % relative to the analytical solution according to the Poiseuille formula and the characteristic relaxation time of the velocity. With synchronous oscillation of piezoelectric elements, a nonzero average fluid flow is a systematic error. This value was compared with the asymmetric oscillation pattern of piezoelectric elements to determine the contribution of the systematic error to the pump-generated liquid flow rate.
Based on the fluid flow velocity profile and the results of profiling the program code, the optimal parameters of the computational grids for the channel (dense uniform) and tube walls (non-uniform, consistent with the velocity profile and reconstructing at each time step) were determined, which reduce the magnitude of the systematic error. The computational meshes for the microchannel and the tube are consistent: the boundary elements on the contact line of the grids coincide. The main way to reduce the error is to increase the density of the computational mesh, which leads to an increase in the required computing resources.
An alternative method is proposed for reducing the systematic error due to an additional pressure drop applied to the channel. Depending on the type of boundary conditions and the number of piezoelectric actuators, this method can reduce the systematic error by 1-2 orders of magnitude without increasing the simulation time. The approach presented in the work to reduce the systematic error will improve the accuracy of modeling the operating modes of a piezoelectric micropump.
References
- Convery N., Gadegaard N. 30 years of microfluidics // Micro and Nano Engineering. 2019. V. 2. Pp. 76–91.
DOI: 10.1016/j.mne.2019.01.003
- Berg J.M., Dallas T. Peristaltic Pumps. Encyclopedia of Microfluidics and Nanofluidics (eds. by Li D.). New York: Springer, 2015. Pp. 2693–2701.
DOI: 10.1007/978-0-387-48998-8_1198
- Microfluidics Based Microsystems: Fundamentals and Applications. Eds. by Kakaç S., Kosoy B., Li D., Pramuanjaroenkij A.
Dordrecht: NATO Science for Peace and Security Series A: Chemistry and Biology. Springer. 2010. 618 p.
DOI: 10.1007/978-90-481-9029-4
- Cotta R.M., Knupp D.C., Naveira-Cotta C.P. Analytical Heat and Fluid Flow in Microchannels and Microsystems. Cham: Springer. 2016. 164 p.
DOI: 10.1007/978-3-319-23312-3
- Darintsev O.V., Migranov A.B. [Capillary micro-grip with feedback] Capilarnyi microzahvat s obratnoi svazju. Patent RF No. 2261795 RU,
[Published] Opublikovano 10.10.2005. Byul. N. 28 (in Russian).
https://www1.fips.ru/registers-doc-view/fips_servlet?DB=RUPAT&DocNumber=2261795&TypeFile=html
- Darintsev O. Microgrippers: Principle of Operation, Construction, and Control Method // In: Ronzhin A., Shishlakov V. (eds) // Proceedings of 15th International
Conference on Electromechanics and Robotics ”Zavalishin’s Readings“. Smart Innovation, Systems and Technologies. 2021. V. 187. Pp. 25–37. Springer, Singapore.
DOI: 10.1007/978-981-15-5580-0_2
- Nasibullayev I.Sh., Darintsev O.V. [Computer 2D modelling of a micro-grip fluid cooling system]. Vychislitel’nyye tekhnologii [Computational technologies]. 2021. V. 26. No. 2. Pp. 4–20.
DOI: 10.25743/ICT.2021.26.2.002
- Laser D.J., Santiago J.G. A review of micropumps // Journal of Micromechanics and Microengineering. 2004. V. 14. Pp. R35–R64.
DOI: 10.1088/0960-1317/14/6/R01
- Fluid-structure Interaction: Modelling, Simulation, Optimization. Eds. by Bungartz H.J., Schäfer M. Heidelberg: Springer. 2006. 401 p.
DOI: 10.1007/3-540-34596-5
- Nasibullayev I.Sh. [The development of a computer model for the main element of the fuel metering unit]. Vychislitel’nye tehnologii [Computational Technologies]. 2016. V. 21, No. 2. Pp. 26–41 (In Russian).
http://www.ict.nsc.ru/jct/getfile.php?id=1724
- Bruus H. Theoretical microfluidics. Lecture notes third edition. MIC Department of Micro and Nanotechnology Technical University of Denmark, 2006. 237 p.
http://homes.nano.aau.dk/lg/Lab-on-Chip2008_files/HenrikBruus_Microfluidics%20lectures.pdf
(дата обращения: 10.05.2020 г.)
- Chiang Ch.-Yu, Pironneau O., Sheu T., Thiriet M. Numerical Study of a 3D Eulerian Monolithic Formulation for Incompressible Fluid-Structures Systems // Fluids. 2017. V. 2, No. 2. P. 34–53.
DOI: 10.3390/fluids2020034
- Hecht F. New development in FreeFem++ // Journal of Numerical Mathematics. 2012. V. 20, No. 3–4. Pp. 251–265.
DOI: 10.1515/jnum-2012-0013
- Nasibullayev I.Sh., Darintsev O.V. Two-dimensional dynamic model of the interaction of a fluid and a piezoelectric bending actuator in a plane channel. Multiphase Systems. 2019. V. 14, No. 4. Pp. 220–232 (in Russian).
DOI: 10.21662/mfs2019.4.029
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Darintsev O.V., [Simulation of fluid flow through a elastic microchannel deformed by a piezoelement in microgrip cooling systems].
Mekhatronika, Avtomatizatsiya, Upravlenie. 2019. V. 20, No. 12. Pp. 740–750 (In Russian).
DOI: 10.17587/mau.20.740-750
- Nasibullayev I.Sh., Darintsev O.V., Nasibullaeva E.Sh. and Bogdanov D.R. Piezoelectric Micropumps for Microrobotics: Operating Modes Simulating and Analysis of the Main Parameters
of the Fluid Flow Generation // In: Ronzhin A. and Shishlakov V. (eds) Proceedings of 15th International Conference on Electromechanics and Robotics ”Zavalishin’s Readings“.
Smart Innovation, Systems and Technologies. 2021. V. 187. Pp. 525–536. Springer, Singapore.
DOI: 10.1007/978-981-15-5580-0_43
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Denisova E.V. [Dynamics of fluid flow in technical systems with jets]. Bulletin of the Ufa Scientific Center of the Russian Academy of Sciences
[Izvestiya Ufimskogo Nauchnogo Centra RAN]. 2015. No. 4. Pp. 20–25 (In Russian).
eLIBRARY ID: 25732231
- Nasibullayev I.Sh., Nasibullaeva E.Sh. [The fluid flow through a system of connected elements of a technical device such as pipe-hydraulic resistance-pipe].
Transactions of the Institute of Mechanics named after R.R. Mavlyutov, Ufa Scientific Center, Russian Academy of Scien [Trudy Instituta mehaniki im. R.R. Mavlyutova,
Ufimskiy Nauchnyi Centr RAN]. 2016. V. 11, No. 2. Pp. 141–149 (In Russian).
DOI: 10.21662/uim2016.2.021
- Nasibullayev I.Sh., Nasibullaeva E.Sh. [Fluid flow through hydraulic resistance with dynamically changing geometry]. Transactions of the Institute of Mechanics named after
R.R. Mavlyutov, Ufa Scientific Center, Russian Academy of Scien [Trudy Instituta mehaniki im. R.R. Mavlyutova]ces, Ufimskiy Nauchnyi Centr RAN]. 2017. V. 12, No. 1. Pp. 59–66 (In Russian).
DOI: 10.21662/uim2017.1.009
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Darintsev O.V. Computer Axisymmetric Model of a Piezoelectric Micropump // Journal of Engineering Science and Technology Review. 2021. V. 14, No. 2. Pp. 152–164.
DOI: 10.25103/jestr.142.19
- Landau L.D., Lifshitz E.M. Theoretical physics. V. 6. Fluid Mechanics. M.: Nauka, 1988. 736 p. (In Russian).
- Sandberg G., Wernberg P.-A., Davidsson P. Fundamentals of Fluid-Structure Interaction // in Computational Aspects of Structural Acoustics and Vibration, CISM International Centre
for Mechanical Sciences. Vol. 505, G. Sandberg and R. Ohayon, Eds. Vienna: Springer, 2009.
DOI: 10.1007/978-3-211-89651-8_2
- Xu J., Lin S., Ma Y., Tang Y. Analysis on Coupled Vibration of a Radially Polarized Piezoelectric Cylindrical Transducer // Sensors. 2017. V. 17, No. 12. P. 2850.
DOI: 10.3390/s17122850
- Wang W., Shi W., Thomas P., Yang M. Design and Analysis of Two Piezoelectric Cymbal Transducers with Metal Ring and Add Mass // Sensors. 2019. V. 19, No. 1. P. 137.
DOI: 10.3390/s19010137
- Murimi E., Kihiu J., Nyakoe G., Mutuli S., Kimotho J. Determination of resonant frequency of a piezoelectric ring for generation of ultrasonic waves //
Innovative Systems Design and Engineering. 2011. V. 2, No. 4. P. 103 (2011).
- Kim J.O., Lee J.G. Dynamic characteristics of piezoelectric cylindrical transducers with radial polarization // Journal of Sound and Vibration. 2007. V. 300, No. 1–2. P. 241.
DOI: 10.1016/j.jsv.2006.08.021
- Nasibullayev I.Sh. Application of free software FreeFem++/Gmsh and FreeCAD/CalculiX for simulation of static elasticity problems. Multiphase Systems. 2020. V. 15. No. 3–4. Pp. 183–200 (In Russian).
DOI: 10.21662/mfs2020.3.129
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Darintsev O.V. Study of fluidflow through a channel deformed by piezoelement. Multiphase Systems. 2018. V. 13, No. 3. Pp. 1–10 (In Russian).
DOI: 10.21662/mfs2018.3.001
- Nasibullayev I.Sh., Nasibullaeva E.Sh. [The effect of temperature on the dynamics of fluid flow in technical systems with jets]. Transactions of the Institute of Mechanics
named after R.R. Mavlyutov, Ufa Scientific Center, Russian Academy of Scien [Trudy Instituta mehaniki im. R.R. Mavlyutova]ces, Ufimskiy Nauchnyi Centr RAN]. 2016. V. 11, No. 1. P. 1–9 (In Russian).
DOI: 10.21662/uim2016.1.001
- Batchelor G.K. An introduction to fluid dynamics. Cambridge University Press. 2000. 615 p.
DOI: 10.1017/CBO9780511800955