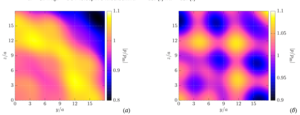
The study of the phenomenon of sound waves scattering by small inhomogeneities, that differ in density and (or) compressibility from the main medium, is one of the important acoustics problems. This is due to the fact that many practical acoustic waves applications are based on this phenomenon, such as hydrolocation, the atmosphere and ocean sounding, creating positionable 3D sound, etc. In the present work, acoustic scattering from a layer consisting of many sound-permeable spheres in 3D space under the monopole radiation source action is investigated. This particular case takes place when a region containing many small inhomogeneities is conventionally two-dimensional (one of three dimensions can be neglected). The problem is solved numerically using a generalized numerical technique based on the fast multipole method, which allows achieving high accuracy of the results with minimal computer time. Verifying the results of the present work, obtained for water droplets in air, within a small error, showed good agreement with similar results of other researchers for soundproof spheres. It is found that a change in the smallest distance between the spheres significantly changes the calculated function values both qualitatively and quantitatively, since the interaction between the spheres highly depends on the density of the sphere arrangement in the configuration. Normalized pressure distribution diagrams, plotted at a distance from the scattering layer, showed that the layer is a two-dimensional diffraction grating analog, which has a different degree of acoustic wave penetration that depends on the ratio of the physical parameters of the external and internal media.
acoustic scattering,
scattering layer,
sound-permeable spheres,
multipole expansion method,
monopole radiation source,
pressure distribution diagram
The study of the phenomenon of sound waves scattering by small inhomogeneities, that differ in density and (or) compressibility from the main medium, is one of the important acoustics problems. This is due to the fact that many practical acoustic waves applications are based on this phenomenon, such as hydrolocation, the atmosphere and ocean sounding, creating positionable 3D sound, etc. In the present work, acoustic scattering from a layer of a simple configuration containing many sound-permeable spheres in 3D space under the action of a spherical wave from a monopole radiation source is investigated. This particular case takes place when a region containing many small inhomogeneities is a conventionally two-dimensional (one of three dimensions can be neglected).
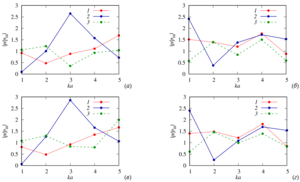
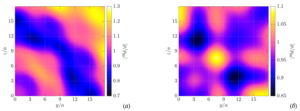
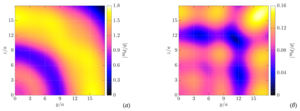
The main goal of the present work is the plotting and analysis of the distribution diagrams of the normalized pressure at a distance from the scattering layer for the various ratios of the physical parameters of the external and internal media, as well as the density of the spheres in the configuration.
The problem is solved within the framework of a computational experiment using a generalized numerical technique based on the fast multipole method. The choice of this method is due to the fact that it allows one to achieve high accuracy of the results need to obtained with minimal CPU time.
The verification of the computer model is carried out: the results of the present work calculated for a layer of water droplets in the air, agree well within a small error with similar results for the small sound-hard spheres obtained by the other researchers.
The following results were obtained:
When constructing these diagrams, the value of the number of the truncation of series during expansion, that provides the necessary accuracy of the calculation, was determined.
Value of the present work is following. The diagrams constructed using the considered approach to the study of acoustic radiation from many spheres, in contrast to the approaches based on averaged equations, make it possible to clearly demonstrate the complete picture of the pressure distribution outside the system of spheres, including for determining the zones of the increasing and decreasing pressure.
In the future, it is planned to conduct studies of the acoustic scattering for the various configurations of the system in a wider range of changes in physical and geometric parameters.