Tukmakov D.A.
Comparison of numerical implementations of the quadrature method for solving an integral equation. Multiphase Systems. 20 (2025) 1. 7–11 (in Russian).
Comparison of numerical implementations of the quadrature method for solving an integral equation
IME KazSC RAS, Kazan, Russia
Abstract
Integral equations are encountered in various sections of physics — in acoustics, filtration theory, in electrophysics, in mechanics of solid
deformable bodies. Fredholm integral equations can be used for mathematical description of processes of radiation and scattering of sound
waves. Often finding an exact analytical solution to integral equations seems difficult, in connection with which numerical methods are used
to solve such equations. This work is devoted to the analysis of algorithms for the numerical solution of the Fredholm integral equation of
the second kind. The paper presents the results of the implementation of some algorithms for the numerical quadrature method for solving
integral equations. The quadrature method reduces the solution of the integral equation to the solution of a system of linear algebraic
equations, which can be implemented in various ways. The choice of the quadrature formula is assumed to be arbitrary; in the study under
consideration, the trapezoid formula was used as a quadrature formula. When reducing an integral equation to a system of linear algebraic
equations, there is also arbitrariness in the choice of the method for solving linear equations. To solve the system of linear equations, the
Gauss method, the method of simple iterations and the iterative Jacobi method were used. The study of the properties of the integral equation
shows that the kernel of the integral operator satisfies the properties under which the integral operator is a contracting operator and,
therefore, the integral equation has a unique solution. Comparison of numerical calculations for various methods of solving a system of linear
equations demonstrates that the Jacobi method for solving a system of linear algebraic equations converges to an exact solution significantly
faster than the method of simple iterations. The results obtained can be used in developing algorithms for solving integral equations.
Keywordsintegral equations,
quadrature method,
system of linear equations
Article outline
For mathematical modeling of fluid and gas mechanics processes, both differential and integral equations are used. The paper (Lukashchuk S.Yu. Fractional-integral generalization of the Rapoport-Lisa equation // Multiphase systems. 2023. Vol. 18. No. 2. Pp. 58-67.) presents a mathematical model of two-phase filtration in a porous medium, based on solving an integro-differential equation. The article (Nasibullaeva E.Sh. Scattering of sound waves on spheres: solution methods and main characteristics (review) // Multiphase systems. 2021. Vol. 16. No. 3-4. Pp. 88-104.) provides an overview of works on theoretical methods for solving problems of scattering of acoustic waves on spheres and determining the main characteristics of this phenomenon. In the publication (Ershov N.E., Illarionova L.V., Smagin S.I. Numerical solution of a three-dimensional stationary problem of acoustic wave diffraction// Computational technologies. 2010. Vol. ~15. No. 1. Pp. 60-76.) methods for numerical solution of spatial problems of stationary acoustic wave diffraction in media with inclusions in a three-dimensional formulation are developed. In the study (Cuha F. A., Peker H. A. Solution of Abel’s integral equation by Kashuri Fundo transform //Thermal Science. 2022. V. 26. No. . 4 Part A. P. 3003-3010.) the development of the theory of analytical methods for solving integral equations as applied to various problems of physics is considered. The work (Antoine X., Darbas M. An introduction to operator preconditioning for the fast iterative integral equation solution of time-harmonic scattering problems // Multiscale Science and Engineering. 2021. V. 3. P. 1-35.) proposes the development of methods for solving integral equations used in various engineering fields. The monograph (Osetrov AV Integral equations in the theory of diffraction of acoustic waves: Textbook. SPb: Publishing house of SPbGETU “LETI”, 2002. 56 p.) describes the application of integral equations in solving various acoustics problems.
From the analysis of works on the topic of integral equations, it follows that both applications of the theory of integral equations for modeling various physical processes and the improvement of methods for solving integral equations are developing.
Fredholm integral equations of the second kind are important for describing the radiation and scattering of acoustic waves. This paper analyzes the application of various algorithms for implementing the quadrature method for numerically solving the Fredholm integral equation of the second kind. The paper investigates the influence of the choice of the integration method for the system of linear equations obtained by the quadrature method on the rate of convergence of the numerical solution of the integral equation.
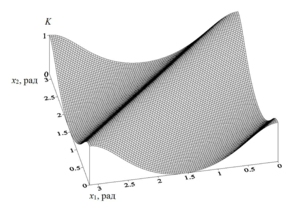
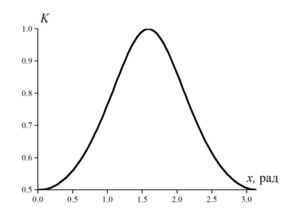
Analysis of the parameters of the kernel of the integral equation shows that the integral operator is contractive (Krasnov M.L. Integral Equations. Moscow: “Nauka”, 1975. 304 p.). Using the numerical quadrature method (the trapezoid formula was considered as a quadrature formula), a system of linear algebraic equations was obtained. To solve the system of equations, the Gauss method, the “simple iteration” method, and the Jacobi method were used.
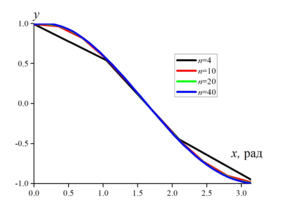
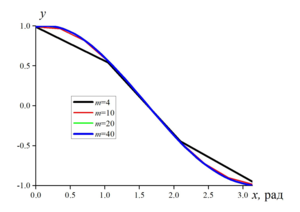
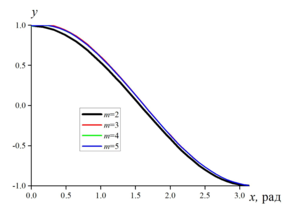
Calculations with different numbers of nodes demonstrate that with an increase in the number of nodes of the quadrature formula, convergence of the numerical solution of the
integral equation is observed. If the system of linear equations is integrated by the Jacobi method, then starting from the value m = 3, the calculation results are close.
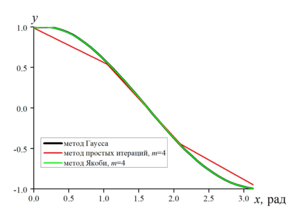
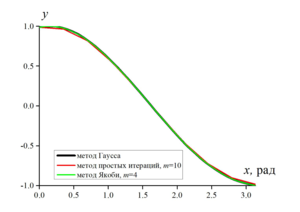
Comparison of the calculation results obtained by the “simple iterations” method and the Jacobi method demonstrates a higher convergence rate when using the Jacobi method.
The paper presents the calculation results of various implementations of the numerical quadrature method for solving the Fredholm integral equation of the second kind.
Comparison of algorithms for solving a system of linear equations obtained as a result of implementing the numerical quadrature method demonstrates that the solution obtained
by the Jacobi method converges faster to the exact solution of the system of linear equations obtained by the Gauss method than the solution obtained by the “simple iterations” method.
The revealed patterns can be used when implementing the quadrature method for solving integral equations in various applied problems.
References
- Тукмаков А.Л. Численное моделирование акустических течений при резонансных колебаниях газа в закрытой трубе // Известия высших
учебных заведений. Авиационная техника. 2006. № 4. С. 33–36.
Tukmakov A.L. Numerical modeling of acoustic flows with resonant oscillations of gas in a closed pipe // Bulletin of higher educational institutions.
Aviation engineering. 2006. No. 4. Pp. 33–36.
EDN: kntxyf
- Тукмаков Д.А. Численное исследование скоростного скольжения фаз при прохождении ударной волны малой интенсивности из чистого газа в
запыленную среду // Многофазные системы. 2019. Т. 14, № 2. С. 125–131.
Tukmakov D.A. Numerical study of high-speed phase sliding during the passage of a low-intensity shock wave from a pure gas into a dusty
environment // Multiphase systems. 2019. V. 14, No. 2. Pp. 125–131.
DOI: 10.21662/mfs2019.2.017
- Тукмаков Д.А. Математическое моделирование взаимодействия ударной волны с электрически заряженной запыленной средой //
Многофазные системы. 2020. Т. 15, № 1–2. С. 101.
Tukmakov D.A. Mathematical modeling of the interaction of a shock wave with an electrically charged dusty environment // Multiphase systems.
2020. V. 15, No. 1–2. Pp. 101 (in Russian).
DOI: 10.21662/mfs2020.1-2
- Тукмаков Д. А. Аналитическая модель нестационарного течения несжимаемой монодисперсной газовзвеси с одномерной геометрией потока //
Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2021. № 3. С. 57–70.
Tukmakov D. A. Analytical model of unsteady flow of an incompressible monodisperse gas suspension with one-dimensional flow geometry //
Bulletin of higher educational institutions. Volga region. Physical and mathematical sciences. 2021. No. 3. Pp. 57–70 (in Russian).
DOI: 10.21685/2072-3040-2021-3-5
- Тукмаков Д.А. Численное моделирование динамики скоплений твердых частиц // Многофазные системы. 2023. Т. 18, № 3. С. 244–246.
Tukmakov D.A. Numerical modeling of the dynamics of solid particle clusters // Multiphase systems. 2023. V. 18, No. 3. Pp. 244–246 (in Russian).
DOI: 10.21662/mfs2023.3.071
- Тукмаков Д.А. Аналитическая модель гравитационного осаждения дисперсной примеси в движущемся потоке // Многофазные системы. 2024.
Т. 19, № 1s. С. 110–112.
Tukmakov D.A. Analytical model of gravitational sedimentation of a dispersed impurity in a moving flow // Multiphase systems. 2024. V. 19, No. 1s.
Pp. 110–112 (in Russian).
DOI: 10.21662/mfs2024.1s
- Лукащук С.Ю. Дробно-интегральное обобщение уравнения Рапопорта–Лиса // Многофазные системы. 2023. Т. 18, № 2. С. 58–67.
Lukashchuk S.Y. Fractional integral generalization of the Rapoport–Lisa equation // Multiphase systems. 2023. V. 18, No. 2. Pp. 58–67 (in Russian).
DOI: 10.21662/mfs2023.2.009
- Насибуллаева Э.Ш. Рассеяние звуковых волн на сферах: методы решения и основные характеристики (обзор) // Многофазные системы. 2021.
Т. 16, № 3–4. С. 88–104.
Nasibullaeva E.Sh. Scattering of sound waves on spheres: solution methods and main characteristics (review) // Multiphase systems. 2021. V. 16,
No. 3–4. Pp. 88–104 (in Russian).
DOI: 10.21662/mfs2021.3.013
- Ершов Н.Е., Илларионова Л.В., Смагин С.И.Численное решение трехмерной стационарной задачи дифракции акустических волн //
Вычислительные технологии. 2010. Т. 15, № 1. С. 60–76.
Ershov N.E., Illarionova L.V., Smagin S.I. Numerical solution of a three-dimensional stationary problem of acoustic wave diffraction // Computational
technologies. 2010. V. 15, No. 1. Pp. 60–76 (in Russian).
EDN: muylnt
- Cuha F.A., Peker H.A. Solution of Abel’s integral equation by Kashuri Fundo transform // Thermal Science. 2022. V. 26, No. 4, Part A. Pp. 3003–3010.
DOI: 10.2298/TSCI2204003C
- Antoine X., Darbas M. An introduction to operator preconditioning for the fast iterative integral equation solution of time-harmonic scattering
problems // Multiscale Science and Engineering. 2021. V. 3. Pp. 1–35.
DOI: 10.1007/s42493-021-00057-6
- Осетров А. В. Интегральные уравнения в теории дифракции акустических волн. Санкт-Петербург: СПбГЭТУ «ЛЭТИ», 2002. 56 с.
Osetrov A. V. Integral equations in the theory of diffraction of acoustic waves. St. Petersburg: SPbGETU ”LETI“, 2002. 56 p. (in Russian).
- Карчевский Е.М. Интегральные уравнения: применение в математическом моделировании, численные методы решения и комплекс программ
на языке MatLab. Казань: Вестфалика, 2022. 89 с.
Karchevsky E.M. Integral equations: application in mathematical modeling, numerical solution methods and a program package in the MatLab
language. Kazan: Vestfalika, 2022. 89 p. (in Russian).
- Краснов М.Л. Интегральные уравнения. Москва: «Наука», 1975. 304 с.
Krasnov M.L. Integral equations. Moscow: «Nauka», 1975. 304 p. (in Russian).
- Авхадиев Ф.Г. Основы численных методов. Казань: Издательство Казанского университета, 2022. 444 с.
Avkhadiev F.G. Fundamentals of numerical methods. Kazan: Kazan University Publishing House, 2022. 444 p. (in Russian).
- Вержбийкий В.М. Вычислительная линейная алгебра. Москва: Высшая школа, 2009. 351 с.
Verzhbiysky V.M. Computational linear algebra. Moscow: Higher School, 2009. 351 p. (in Russian).